题目内容
 2、如下图,在△ABC中,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线,若AD=2cm,则CD=
2、如下图,在△ABC中,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线,若AD=2cm,则CD=4
cm.分析:此题首先根据角平分线的性质可以得到AD=DE,再根据线段垂直平分线的性质得到BD=CD,根据等腰三角形的性质进一步得到∠C=∠DBC=∠ABD=30°,接着可以推出CD=2DE,而AD=2cm,由此即可求出CD的长.
解答:解:∵BD是∠ABC的平分线,∠A=90°,DE是BC的垂直平分线,
∴AD=DE,BD=CD,
∴∠C=∠DBC=∠ABD,
而∠C+∠DBC+∠ABD=180°-∠A=90°,
∴∠C=∠DBC=∠ABD=30°,
∴CD=2DE,
而AD=DE=2,
∴CD=4.
故填4.
∴AD=DE,BD=CD,
∴∠C=∠DBC=∠ABD,
而∠C+∠DBC+∠ABD=180°-∠A=90°,
∴∠C=∠DBC=∠ABD=30°,
∴CD=2DE,
而AD=DE=2,
∴CD=4.
故填4.
点评:此题主要考查线段的垂直平分线的性质和角平分线的性质等几何知识及含30°角的直角三角形的性质;得到30°的角是正确解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 25、如下图,在△ABC中,AD平分外角∠CAE,∠B=30°,∠CAD=65°,则∠ACD等于( )
25、如下图,在△ABC中,AD平分外角∠CAE,∠B=30°,∠CAD=65°,则∠ACD等于( ) 16、如下图,在△ABC中,AB=8,BC=6,AC的垂直平分线MN交AB、AC于点M、N.则△BCM的周长为
16、如下图,在△ABC中,AB=8,BC=6,AC的垂直平分线MN交AB、AC于点M、N.则△BCM的周长为 18、已知如下图,在△ABC中,AB=AC,AD⊥BC,垂足为D,则图中相等的线段还有
18、已知如下图,在△ABC中,AB=AC,AD⊥BC,垂足为D,则图中相等的线段还有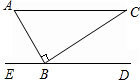 如下图,在△ABC中,∠C=30°,∠ABC=90°,AC∥BD,则∠ABD=
如下图,在△ABC中,∠C=30°,∠ABC=90°,AC∥BD,则∠ABD=