题目内容
【题目】如图,正方形 ABCD 中, G 为 BC 边上一点, BE AG 于 E , DF AG 于 F ,连接 DE .
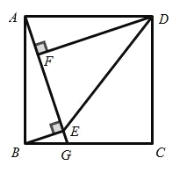
(1)求证: ABE DAF ;
(2)若 AF 1,四边形 ABED 的面积为6 ,求 EF 的长.
【答案】(1)证明见详解;(2)2
【解析】
(1)由∠BAE+∠DAF=90°,∠DAF+∠ADF=90°,推出∠BAE=∠ADF,即可根据AAS证明△ABE≌△DAF;
(2)设EF=x,则AE=DF=x+1,根据四边形ABED的面积为6,列出方程即可解决问题.
证明:(1)∵四边形ABCD是正方形,
∴AB=AD,
∵DF⊥AG,BE⊥AG,
∴∠BAE+∠DAF=90°,∠DAF+∠ADF=90°,
∴∠BAE=∠ADF,
在△ABE和△DAF中
 ,
,
∴△ABE≌△DAF(AAS).
(2)设EF=x,则AE=DF=x+1,
∵S四边形ABED=2S△ABE+S△DEF=6
∴2×![]() ×(x+1)×1+
×(x+1)×1+![]() ×x×(x+1)=6,
×x×(x+1)=6,
整理得:x2+3x-10=0,
解得x=2或-5(舍弃),
∴EF=2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请你估计,当n很大时,摸到白球的频率将会接近 (精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 .
(3)试估算口袋中黑、白两种颜色的球有多少只.