题目内容
【题目】如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至点E,使得OE=OB,交⊙O于点F,连接AE,CE. 
(1)求证:AE是⊙O的切线;
(2)求证:四边形ADCE是矩形;
(3)若BD= ![]() AD=4,求阴影部分的面积.
AD=4,求阴影部分的面积.
【答案】
(1)证明:∵AB=AC,AD是BC边上的中线,
∴∠ODB=90°,
在△BOD和△EOA中,
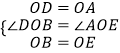 ,
,
∴△BOD≌△EOA,
∴∠OAE=∠ODB=90°,
∵点A在圆上,
∴AE是⊙O的切线;
(2)由(1)知,△BOD≌△EOA,
∴BD=AE,
∵AD是BC边上的中线,
∴CD=BD,
∴AE=CD,
∵∠OAE=∠ODB=90°,
∴AE∥BC,
∴四边形ADCE是平行四边形
∵∠OAE=90°,
∴平行四边形ADCE是矩形;
(3)解:∵∠ODB=90°,BD=OD,
∴∠BOD=45°,
∴∠AOE=45°
∵∠OAE=90°,
∴AE=OA= ![]() AD=4
AD=4
∴S△OAE= ![]() ×OA×AE=
×OA×AE= ![]() ×4×4=8,
×4×4=8,
S扇形OAF=π×42× ![]() =2π,
=2π,
∴S阴影部分=S△OAE﹣S扇形OAF=8﹣2π.
【解析】(1)利用等腰三角形的三线合一的性质,得出∠ODB=90°,从而得出△BOD≌△EOA,得出∠OAE=∠ODB=90°,即可;(2)利用(1)△BOD≌△EOA和三角形的中线得出结论;(3)先判断出AE=OA=4,阴影部分面积用三角形OAE的面积减去扇形OAF的面积即可.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目






