题目内容
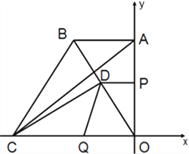
【题目】如图,在直角坐标系中,点A(0,4),B(-3,4),C(-6,0),动点P从点A出发以1个单位/秒的速度在y轴上向下运动,动点Q同时从点C出发以2个单位/秒的速度在x轴上向右运动,过点P作PD⊥y轴,交OB于D,连接DQ.当点P与点O重合时,两动点均停止运动.设运动的时间为t秒.
(1)当t=1时,求线段DP的长;
(2)连接CD,设△CDQ的面积为S,求S关于t的函数解析式,并求出S的最大值;
(3)运动过程中是否存在某一时刻,使△ODQ与△ABC相似?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)S=
;(2)S=![]() ,当
,当![]() 时,S最大值=4;(3)
时,S最大值=4;(3)![]() 和
和![]()
【解析】试题分析:(1)先由题意得到OA=4,AB=3,CO=6,再求出当t=1时,AP、OP的长,最后根据PD⊥y轴,AB⊥y轴,结合平行线分线段成比例即可列比例式求解;
(2)作DE⊥CO于点E,分别用含t的字母表示出CQ、AP、OP,即可表示出DE的长,再根据三角形的面积公式即可得到S关于t的函数解析式,根据二次函数的性质即可求得S的最大值;
(3)分![]() 和
和![]() 两种情况,结合相似三角形的判定方法讨论即可.
两种情况,结合相似三角形的判定方法讨论即可.
(1)由A(0,4),B(-3,4),C(-6,0)可知OA=4,AB=3,CO=6,
当t=1时,AP=1,则OP=3,
∵PD⊥y轴,AB⊥y轴
∴PD∥AB
∴![]()
∴![]()
解得DP=![]() ;
;
(2)CQ=2t,AP=t,OP=4–t
作DE⊥CO于点E,则DE=OP=4–t
∴S=![]() =
=![]() ×2t×(4–t)=
×2t×(4–t)=![]()
当![]() 时,S最大值=4
时,S最大值=4
(3)分两种情况讨论:
①当![]() 时,点Q在CO上运动(当t=3时,△ODQ不存在)
时,点Q在CO上运动(当t=3时,△ODQ不存在)
∵AB∥CO
∴∠BOC=∠ABO<∠ABC
可证得BO=BC
∴∠BOC=∠BCO>∠BCA
∵AB∥CO
∴∠BAC=∠ACO<∠BCO=∠BOC
∴当![]() 时,△ODQ与△ABC不可能相似。
时,△ODQ与△ABC不可能相似。
②当![]() 时,点Q在x轴正半轴上运动,
时,点Q在x轴正半轴上运动,
延长AB,由AB∥CO可得∠FBC=∠BCO=∠BOC,
∴∠ABC=∠DOQ
OQ=![]() ,由DPAB可得OD=
,由DPAB可得OD=![]()
当![]() 时,
时,
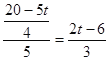 ,
,![]() 在
在![]() 内;
内;
当![]() 时,
时,
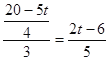 ,
,![]() 在
在![]() 内;
内;
∴存在![]() 和
和![]() ,使△ODQ与△ABC相似。
,使△ODQ与△ABC相似。

 名校课堂系列答案
名校课堂系列答案