��Ŀ����
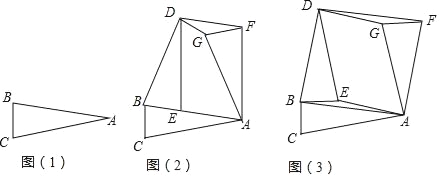
����Ŀ����ͼ1����P��Q�ֱ��DZ߳�Ϊ4cm�ĵȱ�������ABC�ı�AB��BC�ϵĶ��㣬��P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ�Ϊ1cm/s��

��1������AQ��CP���ڵ�M������P��Q�˶��Ĺ����У�֤��![]() ��
��![]() ��
��
��2��![]() �ᷢ���仯�����仯����˵�����ɣ������䣬��������Ķ�����
�ᷢ���仯�����仯����˵�����ɣ������䣬��������Ķ�����
��3��P��Q�˶�����ʱ��![]() ��ֱ�������Σ�
��ֱ�������Σ�
��4����ͼ2������P��Q���˶����յ�����������AB��BC���˶���ֱ��AQ��CP����ΪM����![]() �仯�����仯˵�����ɣ������䣬��������Ķ�����
�仯�����仯˵�����ɣ������䣬��������Ķ�����
���𰸡���1������������2����CMQ=60�㣬���䣻��3������![]() ����2��ʱ����PBQΪֱ�������Σ���4����CMQ=120�㣬���䣮
����2��ʱ����PBQΪֱ�������Σ���4����CMQ=120�㣬���䣮
��������
��1������SAS��֤ȫ�ȣ�
��2����֤��ABQ�ա�CAP���ó���BAQ=��ACP��ͨ���Ƕ�ת�����ɵó���CMQ=60����
��3������2�������һ���ǡ�PQB=90������һ���ǡ�BPQ=90�����ֱ����ֱ�������α�ֱ�ǵĹ�ϵ�����t��ֵ��
��4����֤��PBC�ա�ACQ���Ӷ��ó���BPC=��MQC��Ȼ�����ýǶ�ת���ɵó���CMQ=120����
��1��֤�����ڵȱ�������ABC�У�AB=AC����B=��CAP=60��
������������P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ�Ϊ1cm/s.����֪��
AP=BQ
��![]() ��
��![]() ��
��
��2����CMQ=60������
���ȱ��������У�AB=AC����B=��CAP=60��
����������AP=BQ��
���ABQ�ա�CAP(SAS)��
���BAQ=��ACP��
���CMQ=��ACP+��CAM=��BAQ+��CAM=��BAC=60����
��3����ʱ��Ϊt����AP=BQ=t��PB=4-t��
������PQB=90��ʱ��
�ߡ�B=60����
��PB=2BQ����4-t=2t��t=![]() ��
��
������BPQ=90��ʱ��
�ߡ�B=60����
��BQ=2PQ����2t=2��4-t����t=2��
������![]() ����2��ʱ����PBQΪֱ�������Σ�
����2��ʱ����PBQΪֱ�������Σ�
��4����CMQ=120�����䣬
���ڵȱ��������У�AB=AC����B=��CAP=60����
���PBC=��ACQ=120����
����������BP=CQ��
���PBC�ա�ACQ(SAS)��
���BPC=��MQC��
���ߡ�PCB=��MCQ��
���CMQ=��PBC=180��-60��=120����

 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�