题目内容
【题目】综合与实践
问题情境
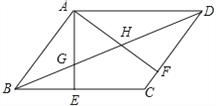
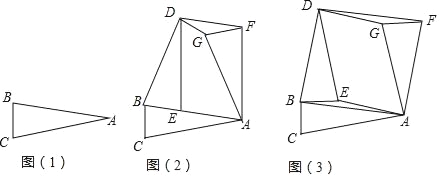
在综合实践课上,老师让同学们“以三角形的旋转”为主题进行数学活动,如图(1),在三角形纸片ABC中,AB=AC,∠B=∠C=α.
操作发现
(1)创新小组将图(1)中的△ABC以点B为旋转中心,逆时针旋转角度α,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转角度α,得到△AFG,连接DF,得到图(2),则四边形AFDE的形状是 .
(2)实践小组将图(1)中的△ABC以点B为旋转中心,逆时针逆转90°,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°,得到△AFG,连接DF、DG、AE,得到图(3),发现四边形AFDB为正方形,请你证明这个结论.
拓展探索
(3)请你在实践小组操作的基础上,再写出图(3)中的一个特殊四边形,并证明你的结论.
【答案】(1)平行四边形;(2)证明见解析(3)四边形AEDG是平行四边形.
【解析】试题分析:(1)由旋转的性质和旋转角度可求得DE∥AF,且DE=AF,可证明四边形AFDE为平行四边形;
(2)由旋转的性质和旋转角度可求得DE∥AF,且DE=AF,可证明四边形AFDE为平行四边形,再由旋转角是90°,即可得出结论;
(3)由旋转的性质和旋转角度判断出△ABE≌△DFG即可得出结论.
试题解析:
(1)证明:∵△DBE是由△ABC绕点B逆时针旋转90°得到的,△AFG是由△ABC绕点A顺时针旋转90°得到的.
∴DE=AC=AF,∠BAF=α,∠DBE=∠ABC=α,∠DEB=∠C=α,
∴∠DEB=∠BAF,
∴DE∥AF,
∵DE=AF,
∴四边形AFDE是平行四边形,
故答案为:平行四边形;
(2)证明:∵△DBE是由△ABC绕点B逆时针旋转90°得到的,△AFG是由△ABC绕点A顺时针旋转90°得到的,
∴∠DBA=∠FAB=90°,DB=AB=AF,
∴∠DBA+∠FAB=180°,
∴DB∥AF,
∵DB=AF,
∴四边形DBAF是平行四边形,
∵∠DBA=90°
∴平行四边形DBAF是正方形.
(3)四边形AEDG是平行四边形.
证明:∵四边形ABDF是正方形,
∴∠DFA=∠DBA=90°,AB=DF,
又∵∠DBE=∠AFG=α,
∴∠EBA=∠GFD.
在△ABE和△DFG中,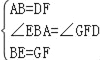 ,
,
∴△ABE≌△DFG,
∴AE=DG,
又∵DE=AG=AB,
∴四边形DEAG是平行四边形.