题目内容
【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”四个类别,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | m | 1 |
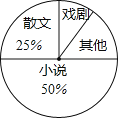
(1)计算m= ;
(2)在扇形统计图中,“其他”类所占的百分比为 ;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的2人恰好是乙和丙的概率.
【答案】(1)40;(2)15%;(3)P(丙和乙)=![]() .
.
【解析】
(1)用散文的频数除以其频率即可求得样本总数;
(2)根据其他类的频数和总人数求得其百分比即可;
(3)画树状图得出所有等可能的情况数,找出恰好是丙与乙的情况,即可确定出所求概率.
(1)∵喜欢散文的有10人,频率为0.25,
∴m=10÷0.25=40;故答案为:40
(2)在扇形统计图中,“其他”类所占的百分比为![]() ,
,
故答案为:15%;
(3)画树状图,如图所示:

所有等可能的情况有12种,其中恰好是丙与乙的情况有2种,
∴P(丙和乙)=![]() .
.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案【题目】“新型冠状病毒肺炎”疫情牵动着亿万国人的心,为进一步加强疫情防控工作,兰州市某学校利用网络平台进行疫情防控知识测试.洪涛同学对九年级1班和2班全体学生的测试成绩数据进行了收集、整理和分析,研究过程中的部分数据如下.
信息一:疫情防控知识测试题共10道题目,每小题10分;
信息二:两个班级的人数均为40人;
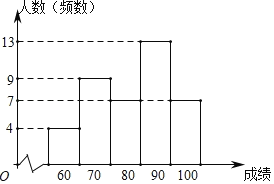
信息三:九年级1班成绩频数分布直方图如图,
信息四:九年级2班平均分的计算过程如下,
![]() 80.5(分);
80.5(分);
信息五:
统计量 班级 | 平均数 | 中位数 | 众数 | 方差 |
九年级1班 | 82.5 | m | 90 | 158.75 |
九年级2班 | 80.5 | 75 | n | 174.75 |
根据以上信息,解决下列问题:
(1)m= ,n= ;
(2)你认为哪个班级的成绩更加稳定?请说明理由;
(3)在本次测试中,九年级1班甲同学和九年级2班乙同学的成绩均为80分,你认为两人在各自班级中谁的成绩排名更靠前?请说明理由.