题目内容
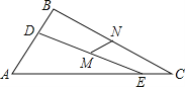
【题目】如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动,当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒.
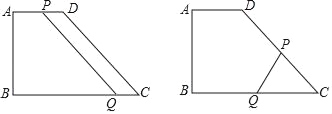
(1)当t为多少秒时,四边形PQCD是平行四边形?请说明理由;
(2)当t为多少秒时,AQ=DC?请说明理由;
(3)当t为多少秒时,PQ⊥DC?请说明理由.
【答案】(1)t=![]() 时,四边形PQCD是平行四边形,理由见解析;(2)当t=
时,四边形PQCD是平行四边形,理由见解析;(2)当t=![]() 或t=4时,AQ=DC,理由见解析;(3)当t=
或t=4时,AQ=DC,理由见解析;(3)当t=![]() 秒,使得PQ⊥DC,理由见解析
秒,使得PQ⊥DC,理由见解析
【解析】
(1)若四边形PQCD是平行四边形,则PD=CQ,根据题意可列出关于t的一元一次方程,求解即可;
(2)过点D作DE⊥BC于点E,则DE=AB=6,利用勾股定理可求出CE的长,从而得出BC=12,BQ=12-5t,在直角△ABQ中利用勾股定理求解即可
(3)利用△CPQ∽△CED求解即可.
解:(1)t=![]() 时,四边形PQCD是平行四边形,理由如下:
时,四边形PQCD是平行四边形,理由如下:
由题意知,AP=4t,CQ=5t,
∴DP=AD﹣AP=4﹣4t,
∵四边形PQCD成为平行四边形,
∴DP=CQ,
∴4﹣4t=5t,
解得:t=![]() ,
,
即t=![]() 时,四边形PQCD是平行四边形;
时,四边形PQCD是平行四边形;
(2)过点D作DE⊥BC于E,连接AQ,
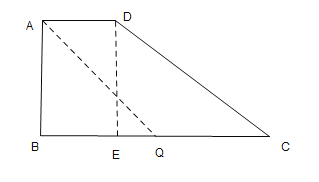
∵∠B=90°,AD∥BC,
∵∠B=90°,AD∥BC,
∴四边形ABED是矩形,
∴DE=AB=6cm,
BE=AD=4cm,
由勾股定理得,CE=![]() ,
,
∴BC=BE+CE=4+8=12cm,
∵CQ=5t,BC=12,
∴BQ=12﹣5t,
∵AQ=CD,
∴![]() ,
,
解得:t=![]() 或t=4(不符合题意,舍去);
或t=4(不符合题意,舍去);
(3)如下图,由题意知,CP=14﹣4t,
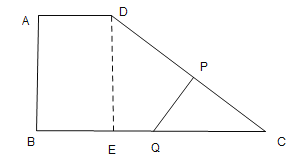
∵PQ⊥CD,
∴∠CPQ=90°,
∴∠CPQ=∠CED,
又∵∠C=∠C,
∴△CPQ∽△CED,
∴![]()
即![]() ,
,
解得t=![]() ,
,
此时,CQ=![]() ×5=
×5=![]() <BC,
<BC,
∴存在t=![]() 秒,使得PQ⊥DC.
秒,使得PQ⊥DC.

 53天天练系列答案
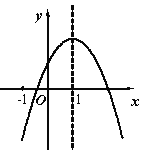
53天天练系列答案【题目】下表给出了代数式﹣x2+bx+c与x的一些对应值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
﹣x2+bx+c | … | 5 | n | c | 2 | ﹣3 | ﹣10 | … |
(1)根据表格中的数据,确定b,c,n的值;
(2)设y=﹣x2+bx+c,直接写出0≤x≤2时y的最大值.
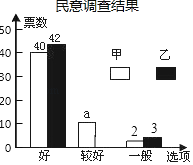
【题目】我校2019年度“一中好声音“校园歌手比赛已正式拉开序幕,其中甲,乙两位同学的表现分外突出,现场A、B、C、D、E、F六位评委的打分情况以及随机抽取的50名同学的民意调查结果分别如下统计表和不完整的条形统计图:
A | B | C | D | E | F | |
甲 | 88 | m | 90 | 93 | 95 | 96 |
乙 | 89 | 92 | 90 | 97 | 94 | 93 |
(1)a= ,六位评委对乙同学所打分数的中位数是 ,并补全条形统计图;
(2)六位评委对甲同学所打分数的平均分为92分,则m= ;
(3)学校规定评分标准:去掉评委评分中最高和最低分,再算平均分,并将平均分与民意测评分按3:2计算最后得分,求甲、乙两位同学的得分,(民意测评分=“好”票数×2+“较好”票数×1+“一般”票数×0)
(4)现准备从甲、乙两位同学中选一位优秀同学代表重庆一中参加市歌手大赛,请问选哪位同学?并说明理由.