题目内容
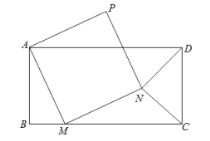
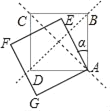
【题目】如图,在菱形ABCD中,点E是BC边上一动点(不与点C重合)对角线AC与BD相交于点O,连接AE,交BD于点G.
(1)根据给出的△AEC,作出它的外接圆⊙F,并标出圆心F(不写作法和证明,保留作图痕迹);
(2)在(1)的条件下,连接EF.①求证:∠AEF=∠DBC;
②记t=GF2+AGGE,当AB=6,BD=6![]() 时,求t的取值范围.
时,求t的取值范围.

【答案】(1)见解析(2)①证明见解析②9≤t≤12
【解析】
(1)作EC的垂直平分线,其与BD的交点即为外心F;
(2)连接AF,EF,利用菱形的性质及外心的定义可证明∠DBC=90°﹣∠ACB及∠AEF=90°﹣∠ACB,可推出结论;
(3)先证△ABG∽△FEG,再证△EFB∽△GFE,由相似三角形的性质可推出t=GF2+AGGE=GF2+GFBG=GF(GF+BG)=GFBF=EF2,在菱形ABCD中,AC⊥BD,EF=AF≥AO,∴EF2≥AO2=32=9,当点F与点O重合时,AF最大,求出此时t的最大值为12,即可写出t的取值范围.
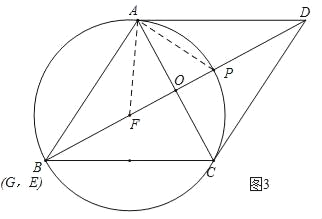
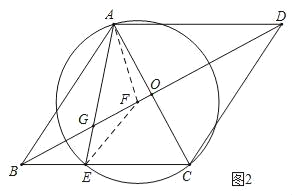
解:(1)如图1,⊙F为所求作的圆;
(2)①证明:
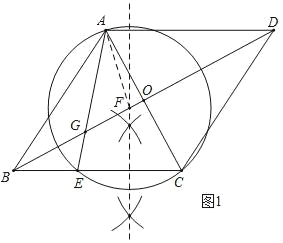
如图2,连接AF,EF,
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠DBC=90°﹣∠ACB,
∵FA=FE,
∴∠AEF=∠FAE,
∴∠AEF=![]() (180°﹣∠AFE)=90°﹣
(180°﹣∠AFE)=90°﹣![]() ∠AFE,
∠AFE,
又∠ACB=![]() ∠AFE,
∠AFE,
∴∠AEF=90°﹣∠ACB,
又∵∠DBC=90°﹣∠ACB,
∴∠AEF=∠DBC;
②解:∵四边形ABCD为菱形,
∴∠ABD=∠CBD,AO=CO,BO=DO=![]() BD=
BD=![]() ×
×![]() ,
,
在Rt△ABO中,AO=![]() ,
,
又∵∠AGB=∠FGE,∠ABG=∠FEG,
∴△ABG∽△FEG,
![]() ,
,
∴AGGE=GFBG,
∵∠GEF=∠FBE,∠GFE=∠EFB,
∴△EFB∽△GFE,
∴![]() ,
,
∴GFBF=EF2,
∴t=GF2+AGGE=GF2+GFBG=GF(GF+BG)=GFBF=EF2,
在菱形ABCD中,AC⊥BD,EF=AF≥AO,
∴EF2≥AO2=32=9,
如图3,当点F与点O重合时,AF最大,
由题意可知:AF=BF,设AF=x,则OF=3![]() ﹣x,
﹣x,
∵AO2+OF2=AF2,
∴32+(3![]() ﹣x)2=x2,
﹣x)2=x2,
解得,x=2![]() ,
,
∴当x=2![]() 时,t的最大值为12,
时,t的最大值为12,
∴9≤t≤12.

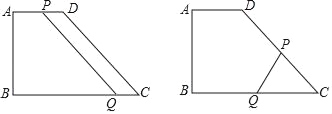
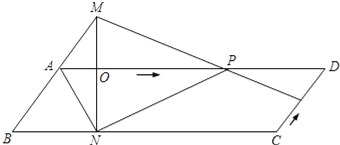
【题目】如图,已知矩形![]() ,点
,点![]() 为线段
为线段![]() 上一动点,沿线段
上一动点,沿线段![]() 由
由![]() 向
向![]() 运动,连接
运动,连接![]() ,以
,以![]() 为边向右侧作正方形
为边向右侧作正方形![]() ,连接
,连接![]() ,设
,设![]() 的路程即
的路程即![]() 的长为
的长为![]() ,
,![]() 间的距离为
间的距离为![]() ,
,![]() 间的距离为
间的距离为![]() .
.
数学兴趣小组的小刚根据学习函数的经验,分别对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行探究,过程如下:
的变化而变化的规律进行探究,过程如下:
(1)根据下表中自变量![]() 的取值进行去电,画图,测量,分别得到几组对应值,请将表格补充完成.
的取值进行去电,画图,测量,分别得到几组对应值,请将表格补充完成.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 2.22 |
| 3 | 4.11 | 5.39 | 6.72 |
| 4.24 | 2.81 | 1.39 | 0 |
| 2.84 | 4.26 |
其中,![]() ,
,![]() ;
;
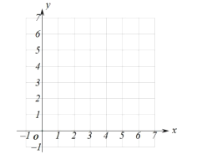
(2)在同一平面黄子佼坐标系中,描点![]() ,并画出
,并画出![]() 的函数图像;
的函数图像;
(3)当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度约为 .
的长度约为 .