Question

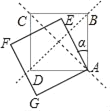
【题目】 如图，△ABC中，∠A=60°，AC＞AB＞2，点D，E分别在边AB，AC上，且BD=CE=2，连接DE，点M是DE的中点，点N是BC的中点，线段MN的长为______．

Answer 1

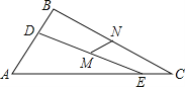
【答案】

【解析】

如图，作CH∥AB，连接DN，延长DN交CH于H，连接EH，作CJ⊥EH于J．首先证明CH=EC，∠ECH=120°，解直角三角形求出EH，利用三角形中位线定理即可解决问题．

解：如图，作CH∥AB，连接DN，延长DN交CH于H，连接EH，作CJ⊥EH于J．

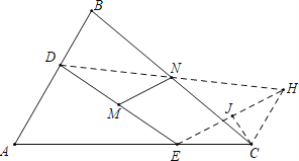
∵BD∥CH，

∴∠B=∠NCH，

∵BN=CN，∠DNB=∠KNC，

∵△DNB≌△HNC（ASA），

∴BD=CH，DN=NH，

∵BD=EC=2，

∴EC=CH=2，

∵∠A+∠ACH=180°，∠A=60°，

∴∠ECH=120°，

∵CJ⊥EH，

∴EJ=JH=ECcos30°=，

∴EH=2EJ=2，

∵DM=ME，DN=NH，

∴MN=EH=．

故答案为．