题目内容
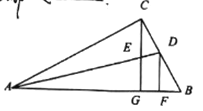
【题目】定义:四条边都相等且四个角都是直角的四边形叫做正方形。我校“快乐走班”数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.
(1)求证:DP=DQ;
(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)如图③,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.
【答案】 (1)证明见解析;(2)猜测:PE=QE.证明见解析; (3)S△DEP =![]() .
.
【解析】试题分析:本题是一道几何证明题,主要考查了正方形的性质、全等三角形的性质与判定、勾股定理等知识点,试题难度不大,但要注意第(3)题中认真计算,避免出错.
求证DP=DQ;只需证明△ADP≌△CDQ即可得到DP=DQ.解题的关键是找出∠PDC的两个余角相等即∠ADP =∠CDQ,两三角形全等的条件就具备了.
PE=QE.只需证明△PDE≌△QDE即可得到,由(1)的结论DP=DQ加上DE是∠PDQ的平分线易用SAS证得结论.
(3)由AB:AP=3:4,AB=6可求AP=8,BP=2;直接由(1)和(2)的结论AP=CQ、PE=QE设CE=x,则PE=8-x,利用勾股定理求得Rt△PEB的边PE,由此可得EQ的长度,这样△DEP的面积就不难求得了.
试题解析:
(1)证明:∵四边形ABCD是正方形
∴DA=DC,∠DAP=∠DCQ=90°
∵∠PDQ=90°
∴∠ADP+∠PDC=90°
∠CDQ+∠PDC=90°
∠ADP=∠CDQ
在△ADP与△CDQ中
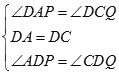
∴△ADP≌△CDQ(ASA)
∴DP=DQ
(2)解:PE=QE.证明如下:
∵ DE是∠PDQ的平分线
∴∠PDE=∠QDE
在△PDE与△QDE中
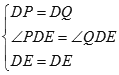
∴△PDE≌△QDE(SAS)
∴PE=QE
(3)解:∵AB:AP=3:4,AB=6
∴AP=8,BP=2,
由(1)知:△ADP≌△CDQ 则AP=CQ=8
由(2)知:△PDE≌△QDE,PE=QE
设CE=x,则PE=QE=CQ-CE=8-x
在Rt△PEB中,BP=2,BE=6+x,PE=8-x
由勾股定理得:22+(6+x)2=(8-x)2
解得:x=![]()
∴![]()
![]()
∴△DEP的面积为:![]()
![]() .
.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案【题目】某中学举行了一次演讲比赛,分段统计参赛同学的成绩,结果如下表(满分100分)
分数段/分 | 61~70 | 71~80 | 81~90 | 91~100 |
人数/人 | 2 | 8 | 6 | 4 |
若已知成绩在91-100分的同学为优胜者.那么优胜率为%。