题目内容
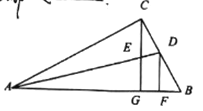
【题目】在△ABC中，AC=BC，∠ACB=90
，CE是过C点的一条直线，AD⊥CE于D，BE⊥CE于E，若DE=6，AD=3，则BE=______．
【答案】3或9
【解析】分为两种情况：
①如图1，
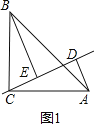
∵AD⊥CE，∠BCA=90°，
∴∠ADC=∠BCA=90°，
∴∠DCA+∠BCE=90°，∠DCA+∠DAC=90°，
∴∠DAC=∠BCE，
∵AD⊥CE，BE⊥CE，
∴∠ADC=∠BEC=90°，
在△ACD和△CBE中，
，
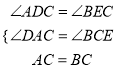∴△ACD≌△CBE（AAS），
∴CE=AD=3，CD=BE，
BE=CD=CE+DE=3+6=9；
②如图2，
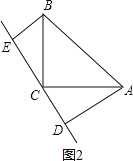
∵在△EBC和△DAC中，
，
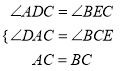∴△ACD≌△CBE（AAS），
∴CE=AD=3，BE=CD，
∴BE=CD=DE-AD=6-3=3，
故答案为：3或9．
练习册系列答案
相关题目
