Question

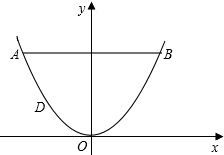
如图所示，一单杠高2.2m，两立柱间的距离为1.6m，将一根绳子的两端拴于立柱与铁杠的结合处A、B，绳子自然下垂，虽抛物线状，一个身高0.7m的小孩站在距立柱0.4m处，其头部刚好触上绳子的D处，求绳子的最低点O到地面的距离．

Answer 1

如图所示，以O为坐标原点，水平方向为x轴，垂直方向为y轴，建立直角坐标系，
设抛物线的解析式为y=ax²（a≠0）．
设A、B、D三点坐标依次为（x_A，y_A），（x_B，y_B），（x_D，y_D），由题意，得AB=1.6，
∴x_A=-0.8，x_B=0.8，又可得x_D=-（

1

2

×1.6-0.4）=-0.4．
∴当x=-0.8时，y_A=a•（-0.8）²=0.64a；
当x=-0.4时，y_D=a•（-0.4）²=0.16a，
∵y_A-y_D=2.2-0.7=1.5，
∴0.64a-0.16a=1.5，
∴a=

25

8

，
∴抛物线解析式为y=

25

8

x²．
当x=-0.4时，y_D=

25

8

×（-0.4）²=0.5，
∴0.7-0.5=0.2m．
答：绳子的最低点距地面0.2m．