题目内容
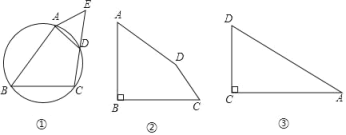
【题目】如图，在ABC中，AC=BC，过C作CD//AB．若AD平分∠CAB，则下列说法错误的是（ ）
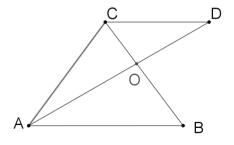
A. BC=CD
B. BO：OC=AB：BC
C. △CDO≌△BAO
D. 
【答案】C
【解析】
A．由角平分线的定义可得出∠CAD=∠BAD，利用“两直线平行，内错角相等”可得出∠CDA=∠BAD，进而可得出∠CAD=∠CDA，由等角对等边结合AC=BC可得出BC=CD，选项A正确；
B．由CD∥AB可得出△AOB∽△DOC，利用相似三角形的性质结合DC=BC，可得出BO：OC=AB：BC，选项B正确；
C．由△CDO∽△BAO，且没有相等的对应边可得出，选项C错误；
D．由三角形的面积公式可得出
，结合相似三角形的性质及平行线的性质可得出
，选项D正确．
A．∵AD平分∠CAB，∴∠CAD=∠BAD．
∵CD∥AB，∴∠CDA=∠BAD，∴∠CAD=∠CDA，∴CD=CA=BC，故选项A正确；
B．∵CD∥AB，∴∠CDO=∠BAO，∠DCO=∠ABO，∴△AOB∽△DOC，∴
，故选项B正确；
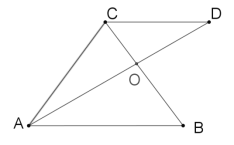
C．∵△CDO∽△BAO，且没有相等的对应边，∴无法证出△CDO≌△BAO，故选项C错误；
D．∵△AOC与△COD同高，∴．
∵△CDO∽△BAO，∴
．
∵AD平分∠CAB，∴∠CAD=∠BAD．
∵CD∥AB，∴∠CDA=∠BAD，∴∠CAD=∠CDA，∴AC=CD．
∵AC=BC，∴CD=BC，∴
，故选项D正确．
故选C．
练习册系列答案
相关题目
