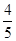题目内容
关于x的方程x2-2(k-1)x+k2 = 0的两实根x1、x2满足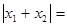 x1x2-1.点A为直线y =" x" 上一点,过A作AC⊥x轴交x轴于C,交双曲线
x1x2-1.点A为直线y =" x" 上一点,过A作AC⊥x轴交x轴于C,交双曲线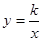 于B,求OB2-AB2的值。
于B,求OB2-AB2的值。
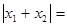 x1x2-1.点A为直线y =" x" 上一点,过A作AC⊥x轴交x轴于C,交双曲线
x1x2-1.点A为直线y =" x" 上一点,过A作AC⊥x轴交x轴于C,交双曲线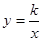 于B,求OB2-AB2的值。
于B,求OB2-AB2的值。k = -3, OB2- AB2 ="-" 6 .
试题分析: ∵方程x2-2(k-1)x+k2 = 0的两实根x1、x2 ,
∴x1+x2 =2(k-1 ), x1x2= k2
∴
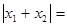 x1x2-1
x1x2-1∴
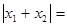
 =
= = k2 -1
= k2 -1∴ k="1" 或 k=-3
又
 =b2 – 4 a c =4(k-1)2 - 4 k2
=b2 – 4 a c =4(k-1)2 - 4 k2 0 即 k
0 即 k 2
2 ∴ k=-3
∴关于x的方程 x2+8x+9=0
∴交双曲线y=

根据题意画出图象:

∵点A为直线y=x上一点,∴AC=CO,
∵OB2=OC2+BC2,AB2=(AC+BC) 2=OC2+BC2+2 OC•BC,
∴OB2-AB2=OC2+BC2-(OC2+BC2+2OC•BC)=-2
 =-2k=-6.
=-2k=-6.点评:本题主要考查了一元二次方程根与系数关系的应用以及一次函数与反比例函数的综合应用,关键是列出关于k的方程以及利用勾股定理得出OB2-AB2=-2OC•BC.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目

 =" x" —1和
=" x" —1和 = —2x + 3.同一坐标系中画出这两个函数的图象.求出这两个函数图象的交点坐标.观察图象,当x取什么范围时,
= —2x + 3.同一坐标系中画出这两个函数的图象.求出这两个函数图象的交点坐标.观察图象,当x取什么范围时,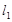 :
: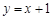 与直线
与直线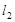 :
: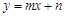 相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 .
相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 .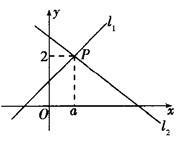
 是∠
是∠ 的边
的边 上一点,且点
上一点,且点