题目内容
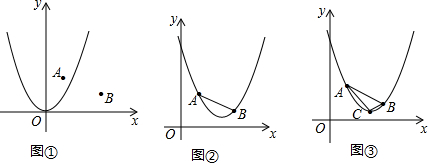
(2012•沙县质检)如图①,在平面直角坐标系中,已知抛物线l1:y=x2和点A(1,2)、B(3,1).
(1)平移抛物线l1,使平移后的抛物线经过点A,写出平移后的一个抛物线的函数表达式;
(2)平移抛物线l1,使平移后的抛物线经过A、B两点,记平移后的抛物线为l2.如图②所示,请在图②上用尺规作图的方式探究抛物线l2上是否存在点P,使△ABP为等腰三角形?若存在,找出满足条件的点P(保留作图痕迹);若不存在,请说明理由;
(3)设抛物线l2的顶点为C,如图③,若K是y轴上一点,且S△ABC=S△AKC,求点K的坐标.
(1)平移抛物线l1,使平移后的抛物线经过点A,写出平移后的一个抛物线的函数表达式;
(2)平移抛物线l1,使平移后的抛物线经过A、B两点,记平移后的抛物线为l2.如图②所示,请在图②上用尺规作图的方式探究抛物线l2上是否存在点P,使△ABP为等腰三角形?若存在,找出满足条件的点P(保留作图痕迹);若不存在,请说明理由;
(3)设抛物线l2的顶点为C,如图③,若K是y轴上一点,且S△ABC=S△AKC,求点K的坐标.

分析:(1)本题答案不唯一,符合条件均可;
(2)应有三点:①以A为圆心,AB为半径作弧可交抛物线l2于一点;②以B为圆心,AB为半径坐标交抛物线于另一点;③作线段AB的垂直平行线可交抛物线于两点,因此共有4个符合条件的P点;
(3)可设出平移后的二次函数的解析式,然后将A、B的坐标代入抛物线的解析式中,即可求得l2的函数表达式,再通过求三角形的面积来求K的坐标.由于△ABC的面积无法直接求出,因此可其转换成其他规则图形面积的和差来解.分别过A、B、C三点作x轴的垂线,因此△ABC的面积可用三个直角梯形的面积差来求出.可先根据直线AB求出其与y轴的交点G的坐标,设出K点坐标后即可表示出KG的长,然后可根据△KBG和△KAG的面积差表示出△KAB的面积,然后根据得出的△ABC的面积即可求出K的坐标.
(2)应有三点:①以A为圆心,AB为半径作弧可交抛物线l2于一点;②以B为圆心,AB为半径坐标交抛物线于另一点;③作线段AB的垂直平行线可交抛物线于两点,因此共有4个符合条件的P点;
(3)可设出平移后的二次函数的解析式,然后将A、B的坐标代入抛物线的解析式中,即可求得l2的函数表达式,再通过求三角形的面积来求K的坐标.由于△ABC的面积无法直接求出,因此可其转换成其他规则图形面积的和差来解.分别过A、B、C三点作x轴的垂线,因此△ABC的面积可用三个直角梯形的面积差来求出.可先根据直线AB求出其与y轴的交点G的坐标,设出K点坐标后即可表示出KG的长,然后可根据△KBG和△KAG的面积差表示出△KAB的面积,然后根据得出的△ABC的面积即可求出K的坐标.
解答:解(1)有多种答案,符合条件即可.
例如y=x2+1,y=2+x,y=(x-1)2+2或y=x2-2x+3,
(2)作图痕迹如图所示.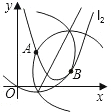
由图可知,点P共有4个可能的位置.
(3)设抛物线l2的函数表达式为y=x2+bx+c,
∵点A(1,2),B(3,1)在抛物线l2上,
∵
,
解得
,
故抛物线l2的函数表达式为y=x2-
x+
=(x-
)2+
,
故C点的坐标为(
,
),
过A,B,C三点分别作x轴的垂线,垂足分别为D,E,F,
则AD=2,CF=
,BE=1,DE=2,DF=
,EF=
,
则S△ABC=S梯形ADEB-S梯形ADFC-S梯形CFEB=
(2+1)×2-
(2+
)×
-
(1+
)×
=
,
延长BA交y轴于点G,设直线AB的函数表达式为y=mx+n,
∵点A(1,2),B(3,1)在直线AB上,
∴
,
解得
,
故直线AB的函数表达式为y=-
x+
,
故G点的坐标为(0,
)
设K点坐标为(0,h),分两种情况:
①若K点位于G点的上方,则KG=h=
,
连接AK,BK.
S△ABK=S△BKG-S△AKG=
×3×(h-
)-
×1×(h-
)=h-
,
∵S△ABK=S△ABC=
,
∴h-
=
,
解得h=
,
则K点的坐标为(0,
)
②若K点位于G点的下方,则KG=h-
,
同理可得,h=
,
则K点的坐标为(0,
),
综上可知K点的坐标为(0,
)或(0,
).
例如y=x2+1,y=2+x,y=(x-1)2+2或y=x2-2x+3,
(2)作图痕迹如图所示.

由图可知,点P共有4个可能的位置.
(3)设抛物线l2的函数表达式为y=x2+bx+c,
∵点A(1,2),B(3,1)在抛物线l2上,
∵
|
解得
|
故抛物线l2的函数表达式为y=x2-
| 9 |
| 2 |
| 11 |
| 2 |
| 9 |
| 4 |
| 7 |
| 16 |
故C点的坐标为(
| 9 |
| 4 |
| 7 |
| 16 |
过A,B,C三点分别作x轴的垂线,垂足分别为D,E,F,
则AD=2,CF=
| 7 |
| 16 |
| 5 |
| 4 |
| 3 |
| 4 |
则S△ABC=S梯形ADEB-S梯形ADFC-S梯形CFEB=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 16 |
| 5 |
| 4 |
| 1 |
| 2 |
| 7 |
| 16 |
| 3 |
| 4 |
| 15 |
| 16 |
延长BA交y轴于点G,设直线AB的函数表达式为y=mx+n,

∵点A(1,2),B(3,1)在直线AB上,
∴
|
解得
|
故直线AB的函数表达式为y=-
| 1 |
| 2 |
| 5 |
| 2 |
故G点的坐标为(0,
| 5 |
| 2 |
设K点坐标为(0,h),分两种情况:
①若K点位于G点的上方,则KG=h=
| 5 |
| 2 |
连接AK,BK.
S△ABK=S△BKG-S△AKG=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
∵S△ABK=S△ABC=
| 15 |
| 16 |
∴h-
| 5 |
| 2 |
| 15 |
| 16 |
解得h=
| 55 |
| 16 |
则K点的坐标为(0,
| 55 |
| 16 |
②若K点位于G点的下方,则KG=h-
| 5 |
| 2 |
同理可得,h=
| 25 |
| 16 |
则K点的坐标为(0,
| 25 |
| 16 |
综上可知K点的坐标为(0,
| 55 |
| 16 |
| 25 |
| 16 |
点评:本题考查了二次函数图象的平移、二次函数解析式的确定、图形面积的求法、等腰三角形的构成情况等知识.综合性强,难度较大.不规则图形的面积通常转化为规则图形的面积的和差进行求解.

练习册系列答案
相关题目
 (2012•沙县质检)如图,点A、B、C在⊙O上,∠AOB=120°,D在AC延长线上,CD=BC,则∠D=
(2012•沙县质检)如图,点A、B、C在⊙O上,∠AOB=120°,D在AC延长线上,CD=BC,则∠D=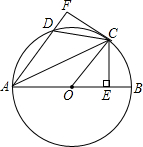 (2012•沙县质检)如图,AB是⊙O的直径,C为⊙O上一点,过点C作CE⊥AB,垂足为E,将△AEC沿AC翻折得到△AFC,AF交⊙O于点D,连接CD、OC.
(2012•沙县质检)如图,AB是⊙O的直径,C为⊙O上一点,过点C作CE⊥AB,垂足为E,将△AEC沿AC翻折得到△AFC,AF交⊙O于点D,连接CD、OC.