题目内容
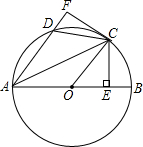 (2012•沙县质检)如图,AB是⊙O的直径,C为⊙O上一点,过点C作CE⊥AB,垂足为E,将△AEC沿AC翻折得到△AFC,AF交⊙O于点D,连接CD、OC.
(2012•沙县质检)如图,AB是⊙O的直径,C为⊙O上一点,过点C作CE⊥AB,垂足为E,将△AEC沿AC翻折得到△AFC,AF交⊙O于点D,连接CD、OC.(1)CF是⊙O的切线吗?请说明理由.
(2)当∠CAE=30°时,判断四边形AOCD是何种特殊四边形,并说明理由.
分析:(1)由折叠的性质,可得∠EAC=∠FAC,∠AFC=∠AEC=90°,又由OA=OC,易证得∠ACO+∠FCA=90°,即可证得CF是⊙O的切线;
(2)由∠CAE=30°,根据折叠的性质与圆周角定理,可证得AD∥OC,△AOD是等边三角形,即可证得四边形AOCD是菱形.
(2)由∠CAE=30°,根据折叠的性质与圆周角定理,可证得AD∥OC,△AOD是等边三角形,即可证得四边形AOCD是菱形.
解答:解:(1)CF是⊙O的切线.理由:
∵将△AEC沿AC翻折得到△AFC,CE⊥AB,
∴∠EAC=∠FAC,∠AFC=∠AEC=90°,
∴∠FAC+∠FCA=90°,
又∵AB是⊙O的直径,C在⊙O上,
∴OA=OC,
∴∠CAO=∠ACO,
∴∠ACO+∠FCA=90°,
即CF⊥OC,
∴CF是⊙O的切线;
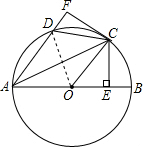 (2)四边形AOCD是菱形.理由:
(2)四边形AOCD是菱形.理由:
连接OD,
∵∠CAE=30°,
∴∠FAO=∠COB=2∠CAE=60°,
∴OC∥AD,
∵OA=OD,
∴△AOD是等边三角形,
∴AD=OA=OC,
∴AD=OC,
∴四边形AOCD是平行四边形,
∴四边形AOCD是菱形.
∵将△AEC沿AC翻折得到△AFC,CE⊥AB,
∴∠EAC=∠FAC,∠AFC=∠AEC=90°,
∴∠FAC+∠FCA=90°,
又∵AB是⊙O的直径,C在⊙O上,
∴OA=OC,
∴∠CAO=∠ACO,
∴∠ACO+∠FCA=90°,
即CF⊥OC,
∴CF是⊙O的切线;
 (2)四边形AOCD是菱形.理由:
(2)四边形AOCD是菱形.理由:连接OD,
∵∠CAE=30°,
∴∠FAO=∠COB=2∠CAE=60°,
∴OC∥AD,
∵OA=OD,
∴△AOD是等边三角形,
∴AD=OA=OC,
∴AD=OC,
∴四边形AOCD是平行四边形,
∴四边形AOCD是菱形.
点评:此题考查了切线的判定、等腰三角形的性质、等边三角形的判定与性质以及菱形的判定.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
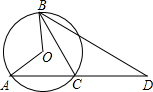 (2012•沙县质检)如图,点A、B、C在⊙O上,∠AOB=120°,D在AC延长线上,CD=BC,则∠D=
(2012•沙县质检)如图,点A、B、C在⊙O上,∠AOB=120°,D在AC延长线上,CD=BC,则∠D=