题目内容
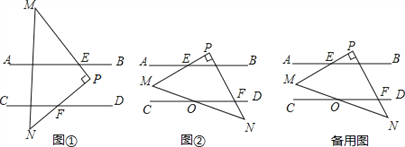
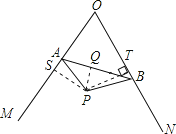
【题目】已知，如图①，∠MON=60°，点A，B为射线OM，ON上的动点（点A，B不与点O重合），且AB=4 
，在∠MON的内部，△AOB的外部有一点P，且AP=BP，∠APB=120°．
（1）求AP的长；
（2）求证：点P在∠MON的平分线上．
（3）如图②，点C，D，E，F分别是四边形AOBP的边AO，OB，BP，PA的中点，连接CD，DE，EF，FC，OP．
①当AB⊥OP时，请直接写出四边形CDEF的周长的值；
②若四边形CDEF的周长用t表示，请直接写出t的取值范围．
【答案】
（1）
解：如图
过点P作PQ⊥AB于点Q．
∵PA=PB，∠APB=120°，AB=4 
∴AQ=BQ=2 ，∠APQ=60°（等腰三角形的“三线合一”的性质），
在Rt△APQ中，sin∠APQ= 
∴AP= 
= 
= 
=4
（2）
证明：过点P分别作PS⊥OM于点S，PT⊥ON于点T．∴∠OSP=∠OTP=90°（垂直的定义）；
在四边形OSPT中，∠SPT=360°﹣∠OSP﹣∠SOB﹣∠OTP=360°﹣90°﹣60°﹣90°=120°，
∴∠APB=∠SPT=120°，∴∠APS=∠BPT；
又∵∠ASP=∠BTP=90°，AP=BP，
∴△APS≌△BPT，
∴PS=PT（全等三角形的对应边相等）
∴点P在∠MON的平分线上；
（3）
解：①∵OP平分∠AOB，∠AOB=60°，OP⊥AB，
∴AQ=BQ= 
AB=2 ，
∴OQ= 
=6，
同理：PQ= 
=2，
∴OP=8，
∵点C，D，E，F分别是四边形AOBP的边AO，OB，BP，PA的中点，
∴CD=EF= AB，CF=DE= OP，
∴四边形CDEF的周长为：8+4
②CD和EF是△ABO和△ABP的中位线，
则CD=EF= AB=2 ，
CF和DE分别是△AOP和△BOP的中位线，则CF=DE= OP，
当AB⊥OP时，OP为四点边形AOBP外接圆的直径时，OP最大，其值是8，OP一定大于当点A或B与点O重合时的长度是4．
则4+4 ＜t≤8+4
【解析】（1）过点P作PQ⊥AB于点Q．根据等腰三角形的“三线合一”的性质推知AQ=BQ= 
AB，然后在直角三角形中利用特殊角的三角函数的定义可以求得AP的长度；（2）作辅助线PS、PT（过点P分别作PS⊥OM于点S，PT⊥ON于点T）构建全等三角形△APS≌△BPT；然后根据全等三角形的性质推知PS=PT；最后由角平分线的性质推知点P在∠MON的平分线上；（3）利用三角形中位线定理知四边形CDEF的周长的值是OP+AB．①当AB⊥OP时，根据直角三角形中锐角三角函数的定义可以求得OP的长度；②当AB⊥OP时，OP取最大值，即四边形CDEF的周长取最大值；当点A或B与点O重合时，四边形CDEF的周长取最小值．
【考点精析】通过灵活运用角平分线的性质定理和三角形中位线定理，掌握定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半即可以解答此题．
