题目内容
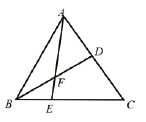
【题目】如图，四边形ABCD内接于⊙O，AB是⊙O的直径，AC和BD相交于点E，且DC2=CECA．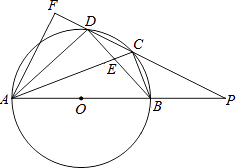 
（1）求证：BC=CD；
（2）分别延长AB，DC交于点P，过点A作AF⊥CD交CD的延长线于点F，若PB=OB，CD= 
，求DF的长．
【答案】
（1）证明：∵DC2=CECA，
∴ 
= 
，
△CDE∽△CAD，
∴∠CDB=∠DAC，
∵四边形ABCD内接于⊙O，
∴BC=CD；
（2）解：方法一：如图，连接OC，
∵BC=CD，
∴∠DAC=∠CAB，
又∵AO=CO，
∴∠CAB=∠ACO，
∴∠DAC=∠ACO，
∴AD∥OC，
∴ 
= 
，
∵PB=OB，CD= 
，
∴ 
= 
∴PC=4 
又∵PCPD=PBPA
∴4 （4 +2 ）=OB3OB
∴OB=4，即AB=2OB=8，PA=3OB=12，
在Rt△ACB中，
AC= 
= 
=2 
，
∵AB是直径，
∴∠ADB=∠ACB=90°
∴∠FDA+∠BDC=90°
∠CBA+∠CAB=90°
∵∠BDC=∠CAB，
∴∠FDA=∠CBA，
又∵∠AFD=∠ACB=90°，
∴△AFD∽△ACB
∴ 
在Rt△AFP中，设FD=x，则AF= 
，
∴在Rt△APF中有， 
，
求得DF= 
．
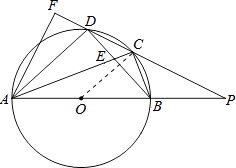
方法二；连接OC，过点O作OG垂直于CD，
易证△PCO∽△PDA，可得 = ，
△PGO∽△PFA，可得 
= ，
可得， = ，由方法一中PC=4 代入 
，
即可得出DF=
【解析】（1）求出△CDE∽△CAD，∠CDB=∠DAC得出结论．（2）连接OC，先证AD∥OC，由平行线分线段成比例性质定理求得PC= 
，再由割线定理PCPD=PBPA求得半径为4，根据勾股定理求得AC= 
，再证明△AFD∽△ACB，得 ，则可设FD=x，AF= ，在Rt△AFP中，利用勾股定理列出关于x的方程，求解得DF．
【考点精析】根据题目的已知条件，利用勾股定理的概念和圆周角定理的相关知识可以得到问题的答案，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半．
