Question

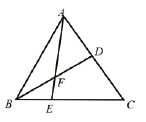
【题目】如图，在△ABC中E是BC上的一点，EC=2BE，点D是AC的中点，设△ABC，△ADF，△BEF的面积分别为且=24，则=___________

Answer 1

【答案】4

【解析】分析: 利用三角形面积公式，等高的三角形的面积比等于底边的比，则S△AEC=S△ABC=16，S△BCD=S△ABC=12，然后利用S△AEC-S△BCD=4即可得到答案.

详解: ：∵EC=2BE，

∴S△AEC=S△ABC=×24=16，

∵点D是AC的中点，

∴S△BCD=S△ABC=×24=12，

∴S△AEC-S△BCD=4，

即S△ADF+S四边形CEFD-（S△BEF-S四边形CEFD）=4，

∴S△ADF-S△BEF=4．

故答案为:4.

点睛: 本题考查了三角形面积：三角形的面积等于底边长与高线乘积的一半，即S△=×底×高；三角形的中线将三角形分成面积相等的两部分.