Question

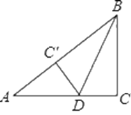
【题目】如图，在Rt△ABC中，∠C=90°，BC=3cm，AC=4cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB边的C′点，那么△ADC′的面积是____．

Answer 1

【答案】

【解析】

先根据勾股定理求出AB的长，再由图形翻折变换的性质得出BC′的长及CD=C′D，设C′D=x，在Rt△ADC′中利用勾股定理即可求出C′D的长，利用三角形的面积公式即可求出△ADC'的面积．

∵在Rt△ABC中，∠C=90°，BC=3，AC=4，
∴AB=

∵△BDC′是△BDC翻折变换而成，BC=3，AC=4，
∴CD=C′D，BC=BC′=3，∠BC′D=90°，
∴∠AC′D=90°，
∴△ADC′是直角三角形，
设C′D=x，则AD=4-x，
在Rt△ADC′中，AD2=AC′2+C′D2，即（4-x）2=（5-3）2+x2，
解得x=

AC′=AB-BC′=5-3=2，
∴S△ADC′=C′D×AC′=××2=

故答案为：