Question

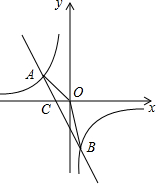
直线y=-x+m与双曲线y=

n

x

交于第四象限一点P（a，b），且a，b是一元二次方程x²-2x-3=0的两根．
（1）求一次函数、反比例函数的解析式；
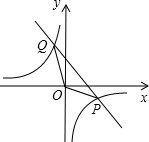
（2）直线与双曲线的另一个交点为Q，求△POQ的面积（O为直角坐标系的原点）．

Answer 1

（1）x²-2x-3=0，
∵点P在第四象限，∴P（3，-1），
把x=3，y=-1代入y=-x+m，y=

n

x

，
得-1=-3+m，m=2，-1=

n

3

，n=-3，
∴y=-x+2，y=

-3

x

=-

3

x

；

（2）y=-x+2
∴y=-

3

x

∴-x+2=-

3

x

-x²+2x=-3
∴x²-2x-3=0
∴（x-3）（x+1）=0
∴x₁=3，x₂=-1
当x=3时，y=-3+2=-1，当x=-1时，y=1+2=3
∴

x1=3 y1=-1

x2=-1 y2=3

∴P（3，-1），Q（-1，3）
∴S_△POQ=4．