题目内容
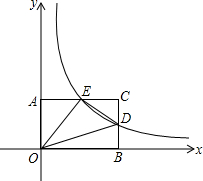
如图，反比例函数y=
（x＞0）的图象上有A、B两点，过A作AD⊥x轴于D，过B作BC⊥x轴于C点，若AD=3BC，求四边形ABCD的面积．
| 6 |
| x |
设点B的坐标为（a，
)，∴BC=
，
∵AD=3BC，∴AD=
，
则点A的纵坐标为
．点A的坐标为（
，
）．
∵点A，B的坐标为（
，
）、（a，
）且AD⊥x轴于D，BC⊥x轴于C，则点D，C的坐标分别为（
，0)、（a，0）
∴CD=a-
=
，
∴四边形ABCD的面积=
=
=8．
| 6 |
| a |
| 6 |
| a |
∵AD=3BC，∴AD=
| 18 |
| a |
则点A的纵坐标为
| 18 |
| a |
| a |
| 3 |
| 18 |
| a |
∵点A，B的坐标为（
| a |
| 3 |
| 18 |
| a |
| 6 |
| a |
| a |
| 3 |
∴CD=a-
| a |
| 3 |
| 2a |
| 3 |
∴四边形ABCD的面积=
| (AD+BC)×CD |
| 2 |
(
| ||||||
| 2 |
练习册系列答案
相关题目
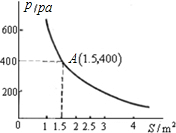当压力不变时，木板对地面的压强p（Pa）是木板面积S（m2）的反比例函数，其图象如图所示．
