题目内容
【题目】如图1,在平面直角坐标系中A(a,0),B(0,b),且a,b满足![]() .
.


(1) (2)
(1)A、B坐标分别为A( ) 、B( ).
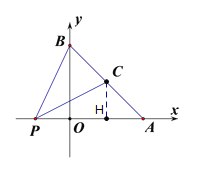
(2)P为x轴上一点,C为AB中点,∠APC=∠PBO,求AP的长.
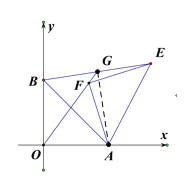
(3)如图2,点E为第一象限一点,AE=AB,以AE为斜边构造等腰直角△AFE,连BE,连接OF并延长交BE于点G,求证:BG=EG.
【答案】(1)A(4,0),B(0,4);(2)6;(3)见解析.
【解析】
(1)根据![]() 解出a,b的值,即可求出A,B的坐标;
解出a,b的值,即可求出A,B的坐标;
(2)作CH⊥AP于点H,由△AOB为等腰直角三角形,可证明∠PBC=∠PCB,从而证明△PBO≌△CPH,即可求出AP长;
(3)连接AG,根据题意证明△AOB≌△AFE,再根据角度转换得到∠BGO,∠AGO的度数,即可证明∠AGB=90°,即可证明BG=EG.
(1)由![]() 得:a=b=4,
得:a=b=4,
则点A坐标为(4,0),点B坐标为(0,4);
(2)作CH⊥AP于点H,
由(1)知△AOB为等腰直角三角形,
∴∠OBA=∠OAB=45°,
∵∠APC=∠PBO,
∴∠PCB=∠APC+∠CAP,∠PBC=∠PBO+∠OBA,
∴∠PBC=∠PCB,
∴PB=PC,
在△PBO和△CPH中
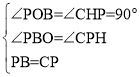
∴△PBO≌△CPH(AAS),
∵C为AB中点,
∴CH=2,
∴PO=CH=2,
∴AP=OA+OP=4+2=6;
(3)连接AG,
∵△AFE为等腰直角三角形,AE=AB,
在△AOB和△AFE中
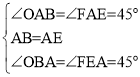
∴△AOB≌△AFE(ASA),
∴∠OAF=∠BAE,
∴∠FOA=∠EBA,
∴∠BGO=∠OAB=45°,
∴∠BOF=∠BAG,
∴∠AGO=∠OBA=45°,
∴∠BGA=90°,
∵△ABE为等腰三角形,
根据等腰三角形的三线合一知G为BE中点,
∴BG=EG.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目







