题目内容
如图∠AOC=∠COD=∠DOB,且OD⊥OA,OC⊥OB,则∠AOB= 度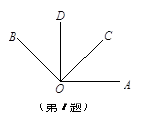

135
由已知OD⊥OA,OC⊥OB可得:∠BOC=90°,∠AOD=90°,则∠DOB+∠COD=90°,∠AOC+∠COD=90°再由已知∠AOC=∠COD=∠DOB,通过等量代换求出一个角的度数,再乘以3即得答案.
解:∵OD⊥OA,OC⊥OB,
∴∠BOC=90°,∠AOD=90°,
则∠DOB+∠COD=90°,∠AOC+∠COD=90°,
又∠AOC=∠COD=∠DOB,
∴∠DOB+∠COD=90°即2∠COD=90°,
∴∠COD=45°,
∴∠AOC=∠COD=∠DOB=45°,
∠AOB=∠AOC+∠COD+∠DOB=45°+45°+45°=135°.
故答案为:135.
解:∵OD⊥OA,OC⊥OB,
∴∠BOC=90°,∠AOD=90°,
则∠DOB+∠COD=90°,∠AOC+∠COD=90°,
又∠AOC=∠COD=∠DOB,
∴∠DOB+∠COD=90°即2∠COD=90°,
∴∠COD=45°,
∴∠AOC=∠COD=∠DOB=45°,
∠AOB=∠AOC+∠COD+∠DOB=45°+45°+45°=135°.
故答案为:135.

练习册系列答案
相关题目
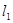 为
为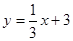 与直线
与直线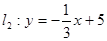 相交于A点,直线
相交于A点,直线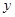 轴于B点,直线
轴于B点,直线 交
交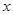 轴于C点,求 ① A点的坐标; ② △ABC的面积。
轴于C点,求 ① A点的坐标; ② △ABC的面积。

 的绳子围成一个长方形,且长方形的长比宽长10
的绳子围成一个长方形,且长方形的长比宽长10
 与
与 互余,且
互余,且 ,则
,则