题目内容
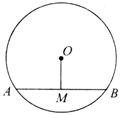
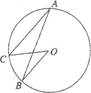
如图,AB是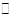 O的直径,点D在
O的直径,点D在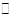 O上∠AOD=130°,BC∥OD交
O上∠AOD=130°,BC∥OD交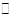 O于C,则∠A= ▲ .
O于C,则∠A= ▲ .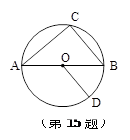
 O的直径,点D在
O的直径,点D在 O上∠AOD=130°,BC∥OD交
O上∠AOD=130°,BC∥OD交 O于C,则∠A= ▲ .
O于C,则∠A= ▲ .
40°
已知∠AOD的度数,即可求出其补角∠BOD的度数;根据平行线的内错角相等,易求得∠B的度数;由于AB是直径,由圆周角定理知∠ACB是直角,则∠A、∠B互余,由此得解.
解:∵∠AOD=130°,
∴∠BOD=50°;
∵BC∥OD,
∴∠B=∠BOD=50°;
∵AB是⊙O的直径,
∴∠ACB=90°;
∴∠A=90°-∠B=40°.
解:∵∠AOD=130°,
∴∠BOD=50°;
∵BC∥OD,
∴∠B=∠BOD=50°;
∵AB是⊙O的直径,
∴∠ACB=90°;
∴∠A=90°-∠B=40°.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 中,CD是直径,AB是弦,
中,CD是直径,AB是弦,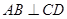 于M,
于M,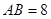 ,
,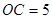 ,则MD的长为( )
,则MD的长为( )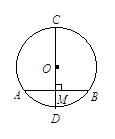
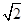
 m
m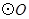 的弦
的弦 ,
,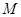 是
是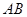 的中点,且
的中点,且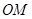 为
为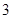 ,则
,则