题目内容
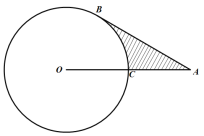
【题目】如图,AB为⊙O的直径,弦CF⊥AB于点E,CF=4![]() ,过点C作⊙O的切线交AB的延长线于点D,∠D=30°,则OA的长为( )
,过点C作⊙O的切线交AB的延长线于点D,∠D=30°,则OA的长为( )
A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 4
D. 4![]()
【答案】B
【解析】
由∠D=30°,利用切线的性质可得∠COB的度数,利用等边三角形的判定和性质及切线的性质可得∠BCD,易得BC=BD,由垂径定理得CE的长,在直角三角形COE中,利用锐角三角函数易得OC的长,得BD的长.
解:连结CO,BC,
∵CD切⊙O于C,
∴∠OCD=90°,
又∵∠D=30°,
∴∠COB=60°,
∴△OBC是等边三角形,即BC=OC=OB,
∴∠BCD=90°﹣∠OCB=30°,
∴BC=DB,
又∵直径AB⊥弦CF,
∴直径AB平分弦CF,即CE=![]() ,
,
在Rt△OCE中,sin∠COE=![]() =
=![]() ,
,
∴OC=![]() =4,
=4,
∴OA=OC=4.
故选:B.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目