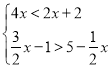题目内容
【题目】成都市空气质量整治领导小组近期提出“保护好环境,拒绝冒黑烟”.某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买![]() 型和
型和![]() 型两种环保节能的公交车10辆.若购买
型两种环保节能的公交车10辆.若购买![]() 型公交车1辆,
型公交车1辆,![]() 型公交车2辆,共需400万元;若购买
型公交车2辆,共需400万元;若购买![]() 型公交车2辆,
型公交车2辆,![]() 型公交车1辆,共需350万元.
型公交车1辆,共需350万元.
(1)求购买![]() 型和
型和![]() 型公交车每辆各需多少万元?
型公交车每辆各需多少万元?
(2)预计在该线路上![]() 型和
型和![]() 型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买
型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买![]() 型和
型和![]() 型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少费用是多少?
型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少费用是多少?
【答案】(1)购买A型公交车每辆需100万元,购买B型公交车每辆需150万元;(2)有三种购买方案①购买A型公交车6辆,则B型公交车4辆;②购买A型公交车7辆,则B型公交车3辆;③购买A型公交车8辆,则B型公交车2辆;购买A型公交车8辆,B型公交车2辆费用最少,最少总费用为1100万元.
【解析】
(1)设购买A型公交车每辆需x万元,购买B型公交车每辆需y万元,根据“A型公交车1辆,B型公交车2辆,共需400万元;A型公交车2辆,B型公交车1辆,共需350万元”列出方程组解决问题;
(2)设购买A型公交车a辆,则B型公交车(10-a)辆,由“购买A型和B型公交车的总费用不超过1200万元”和“10辆公交车在该线路的年均载客总和不少于680万人次”列出不等式组,解不等式组即可得出答案.
解:(1)设购买A型公交车每辆需x万元,购买B型公交车每辆需y万元,由题意得
![]() ,
,
解得![]() ,
,
答:购买A型公交车每辆需100万元,购买B型公交车每辆需150万元.
(2)设购买A型公交车a辆,则B型公交车(10-a)辆,由题意得
![]() ,
,
解得:6≤a≤8,
所以a=6,7,8;
则(10-a)=4,3,2;
所以有三种购买方案:
①购买A型公交车6辆,则B型公交车4辆:100×6+150×4=1200万元;
②购买A型公交车7辆,则B型公交车3辆:100×7+150×3=1150万元;
③购买A型公交车8辆,则B型公交车2辆:100×8+150×2=1100万元;
所以购买A型公交车8辆,B型公交车2辆费用最少,最少总费用为1100万元.