��Ŀ����
����Ŀ���Ŷ���ƻ�����A��B������Ṳ42����Ϊ��ҵ��Ʒ����֪A�����ĵ��۱�B�ֵĶ�10Ԫ����4��A���������5��B�����ķ�����ͬ��
��1����A��B�������ĵ��۷ֱ��Ƕ���Ԫ��
��2������ѧ�����������ϲ�ò�ͬ���������֪�������A����������Ҫ����B�����������![]() �����ֲ�����B�����������
�����ֲ�����B�����������![]() ���������A�����x�ᣮ
���������A�����x�ᣮ
���ж����ֲ�ͬ�Ĺ�����
���̵�Ϊ�˴�����������A�����ÿ������aԪ���ۣ�12��a��18����B�����ÿ������bԪ���ۣ�����ί��ͬѧ�ڸ���ʱ���֣�����������ܷ����빺��ķ����أ����ܷ�������ʱ�����ʱa��ֵ��
���𰸡���1��A�����ĵ���Ϊ50Ԫ��B�����ĵ���Ϊ40Ԫ����2����x��ȡ12��13��14��15��16��17����6�ֲ�ͬ�Ĺ�������18��
��������
(1)��A�����ĵ���ΪmԪ��B�����ĵ���ΪnԪ�����ݡ�A�����ĵ��۱�B�ֵĶ�10Ԫ����4��A���������5��B�����ķ�����ͬ�������ɵó�����m��n�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
(2)�����ݡ������A����������Ҫ����B�����������![]() �����ֲ�����B�����������
�����ֲ�����B�����������![]() �������ɵó�����x��һԪһ�β���ʽ�飬��֮���ɵó�x��ȡֵ��Χ���ٽ��xΪ���������ɵó�x�Ŀ���ֵ�������ɵó�������������
�������ɵó�����x��һԪһ�β���ʽ�飬��֮���ɵó�x��ȡֵ��Χ���ٽ��xΪ���������ɵó�x�Ŀ���ֵ�������ɵó�������������
���蹺���ܷ���ΪwԪ�������ܼۣ����ۡ����������ɵó�w����x�ĺ�����ϵʽ���ɹ���������ܷ����빺��ķ����ؿɵó�b��a��10�������ɵó�w����a�ĺ�����ϵʽ��������һ�κ��������ʣ����ɽ����ֵ���⣮
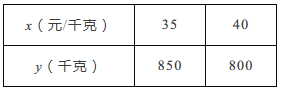
�⣺��1����A�����ĵ���ΪmԪ��B�����ĵ���ΪnԪ��
�����⣬�ã�![]() ��
��
��ã�![]() ��
��
��A�����ĵ���Ϊ50Ԫ��B�����ĵ���Ϊ40Ԫ��
��2�������ݹ����A����������Ҫ����B�����������![]() �����ֲ�����B�����������
�����ֲ�����B�����������![]() �ã�
�ã�
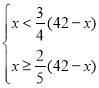 ��
��
��ã�12��x��18��
�֡�xΪ��������
��x��ȡ12��13��14��15��16��17����6�ֲ�ͬ�Ĺ�����
���蹺���ܷ���ΪwԪ��
������ã�w��(50��a��x+(40��b)(42��x)��(10��a+b)x+42(40��b)��
�߹���������ܷ����빺��ķ����أ���w��ֵ��x�أ�
��10��a+b��0��
��b��a��10��
��w��42(40-b)��42[40-(a-10)]����42a+2100��
�ߩ�42��0��
��w��a�����������
�֡�12��a��18��
�൱a��18ʱ��wȡ����Сֵ��
�𣺵��ܷ�������ʱ��a��ֵΪ18��

 ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д� ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�