Question

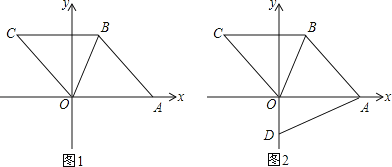
【题目】平面直角坐标系中，四边形ABCO是菱形，点C的坐标为（﹣3，4），点A在x轴的正半轴上，O为坐标原点，连接OB，抛物线y＝ax2+bx+c经过C、O、A三点．

（1）直接写出这条抛物线的解析式；

（2）如图1，对于所求抛物线对称轴上的一点E，设△EBO的面积为S1，菱形ABCO的面积为S2，当S1≤S2时，求点E的纵坐标n的取值范围；

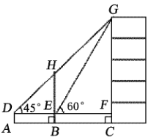
（3）如图2，D（0，﹣）为y轴上一点，连接AD，动点P从点O出发，以个单位/秒的速度沿OB方向运动，1秒后，动点Q从O出发，以2个单位/秒的速度沿折线O﹣A﹣B方向运动，设点P运动时间为t秒（0＜t≤6），是否存在实数t，使得以P、Q、B为顶点的三角形与△ADO相似？若存在，求出相应的t值；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）0≤n≤10且n≠5；（3）t的值为2或．

【解析】

（1）求得菱形的边长，则A的坐标可以求得，然后利用待定系数法即可求得函数的解析式；

（2）首先求得菱形的面积，即可求得S1的范围，当S1取得最大值时即可求得直线的解析式，则n的值的范围即可求得；

（3）分当1＜t＜3.5时和3.5≤t≤6时两种情况进行讨论，依据相似三角形的对应边的比相等，即可列方程求解．

解：（1）∵C点坐标为（﹣3，4），四边形ABCD是菱形，

∴OA＝OC＝＝5，A点坐标为（5，0），

根据题意，将C、O、A三点代入y＝ax2+bx+c中得：

，

解得：，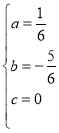

则抛物线的解析式是：；

（2）设BC与y轴相交于点G，则S2＝OGBC＝20，

∴S1≤5，

由C点坐标为（﹣3，4）和CB=5可得B点坐标为（2，4），

所以OB所在直线的解析式是y＝2x，OB＝，

∴当S1＝5时，△EBO的OB边上的高是．

如图1，设平行于OB的直线为y＝2x+b，则它与y轴的交点为M（0，b），与抛物线对称轴x＝交于点E（，n）．

过点O作ON⊥ME，点N为垂足，若ON＝，

∵ME//OB，

∴△MNO∽△OGB，得OM＝5，

∴y＝2x﹣5，

将代入y＝2x﹣5中，解得：y＝0，

即E的坐标是（，0）．

∵与OB平行且到OB的距离是的直线有两条．

∴由对称性可得另一条直线的解析式是：y＝2x+5．

则E′的坐标是（，10）．

由题意得得，n的取值范围是：0≤n≤10且n≠5．

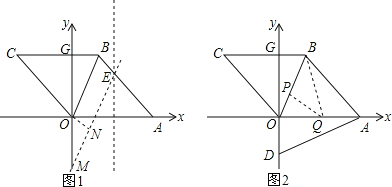
（3）如图2，动点P、Q按题意运动时，

当1＜t＜3.5时，

OP＝t，BP＝2﹣t，OQ＝2（t﹣1），

连接QP，当QP⊥OP时，有＝sin∠BOQ＝sin∠OBC＝，

∴PQ＝（t﹣1），

若＝，则有＝，

又∵∠QPB＝∠DOA＝90°，

∴△BPQ∽△AOD，

此时，PB＝2PQ，即2﹣t＝（t﹣1），

10﹣t＝8（t﹣1），

∴t＝2；

当3.5≤t≤6时，QB＝10﹣2（t﹣1）＝12﹣2t，如图连接QP．

如图3，若QP⊥BP，

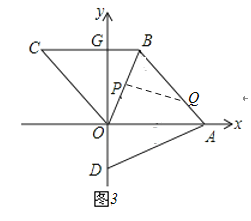
则有∠PBQ＝∠ODA，

又∵∠QPB＝∠AOD＝90°，

∴△BPQ∽△DOA，

此时，QB＝PB，即12﹣2t＝（2﹣t），12﹣2t＝10﹣t，

∴t＝2（不合题意，舍去）．

如图4，若QP⊥BQ，则△BPQ∽△DAO，

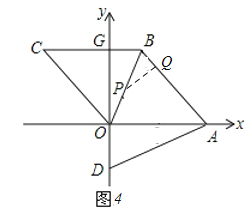
此时，PB＝BQ，

即2﹣t＝（12﹣2t），2﹣t＝12﹣2t，

解得：t＝．

则t的值为2或．