Question

【题目】如图,已知F,G是OA上两点,M,N是OB上两点,且FG=MN,△PFG和△PMN的面积相等.试判断点P是否在∠AOB的平分线上,并说明理由.

Answer 1

【答案】.解:点P在∠AOB的平分线上.理由:如图,过P分别作PD⊥OA于点D,PE⊥OB于点E.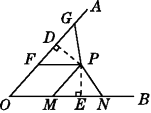

∵S△PFG= FG·PD,S△PMN= MN·PE,
S△PFG=S△PMN,
∴ FG·PD= MN·PE.
又∵FG=MN,
∴PD=PE.
∴点P在∠AOB的平分线上.
【解析】点P在∠AOB的平分线上.理由:如图,过P分别作PD⊥OA于点D,PE⊥OB于点E.根据面积法得出S△PFG= FG·PD,S△PMN= MN·PE,又因S△PFG=S△PMN,FG=MN，从而得出PD=PE.根据到角两边距离相等的点在这个角的角平分线上得出点P在∠AOB的平分线上.