题目内容
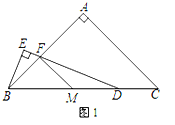
【题目】如图，已知在Rt△ABC中，∠ABC=90°，点D是BC边的中点，分别以B、C为圆心，大于线段BC长度一半的长为半径画弧，两弧在直线BC上方的交点为P，直线PD交AC于点E，连接BE，则下列结论：①ED⊥BC；②∠A=∠EBA；③EB平分∠AED；④ED=
AB中，一定正确的是（ ）
A. ①②③ B. ①②④ C. ①③④ D. ②③④
【答案】B
【解析】根据作图过程得到PB=PC，然后利用D为BC的中点，得到PD垂直平分BC，从而利用垂直平分线的性质对各选项进行判断即可．
解：根据作图过程可知：PB=CP，
∵D为BC的中点，
∴PD垂直平分BC，
∴①ED⊥BC正确；
∵∠ABC=90°，
∴PD∥AB，
∴E为AC的中点，
∴EC=EA，
∵EB=EC，
∴②∠A=∠EBA正确；③EB平分∠AED错误；④ED=
AB正确，
故正确的有①②④，
故选B．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
