题目内容
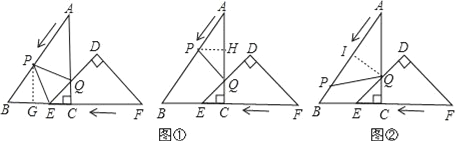
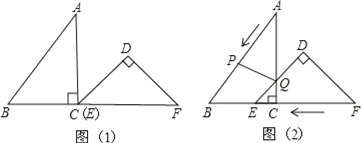
【题目】把Rt△ABC和Rt△DEF按如图（1）摆放（点C与E重合），点B、C（E）、F在同一条直线上．已知：∠ACB=∠EDF=90°，∠DEF=45°，AC=8cm，BC=6cm，EF=10cm．如图（2），△DEF从图（1）的位置出发，以1cm/s的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△ABC的顶点A出发，以2cm/s的速度沿AB向点B匀速移动；当点P移动到点B时，点P停止移动，△DEF也随之停止移动．DE与AC交于点Q，连接PQ，设移动时间为t（s）．
（1）用含t的代数式表示线段AP和AQ的长，并写出t的取值范围；
（2）连接PE，设四边形APEQ的面积为y（cm2），试探究y的最大值；
（3）当t为何值时，△APQ是等腰三角形．
【答案】（1）AP=2t，AQ=8﹣t，t的取值范围是：0≤t≤5；（2）
cm2；（3）
或
或
时，△APQ是等腰三角形．
【解析】试题分析：（1）根据题意以及直角三角形性质表达出CQ、AQ，从而得出结论，
（2）作PG⊥x轴，将四边形的面积表示为S△ABC﹣S△BPE﹣S△QCE即可求解，
（3）根据题意以及三角形相似对边比例性质即可得出结论．
（1）解：AP=2t
∵∠EDF=90°，∠DEF=45°，
∴∠CQE=45°=∠DEF，
∴CQ=CE=t，
∴AQ=8﹣t，
t的取值范围是：0≤t≤5；
（2）过点P作PG⊥x轴于G，可求得AB=10，SinB=
，PB=10﹣2t，EB=6﹣t，
∴PG=PBsinB=
（10﹣2t）
∴y=S△ABC﹣S△PBE﹣S△QCE=
= 
=
∴当
（在0≤t≤5内），y有最大值，y最大值=
（cm2）
（3）若AP=AQ，则有2t=8﹣t解得： 
（s）
若AP=PQ，如图①：过点P作PH⊥AC，则AH=QH=
，PH∥BC
∴△APH∽△ABC，
∴
，
即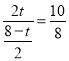
，
解得： 
（s）
若AQ=PQ，如图②：过点Q作QI⊥AB，则AI=PI=
AP=t
∵∠AIQ=∠ACB=90°∠A=∠A，
∴△AQI∽△ABC
∴
即
，
解得： 
（s）
综上所述，当
或
或
时，△APQ是等腰三角形．
