题目内容
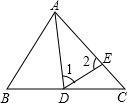
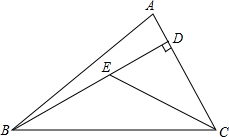
如图，△ABC中，BD⊥AC于D，若∠A+∠ABC=140°，∠A-∠ABC=20°，E为线段BD上任意一点．
（1）求∠ABD的度数．（2）试说明为什么∠BEC＞∠A．
（1）求∠ABD的度数．（2）试说明为什么∠BEC＞∠A．
（1）∵∠A+∠ABC=140°，∠A-∠ABC=20°，
∴∠A=80°，∠ABC=60°，
又∵BD⊥AC，
∴∠ADB=90°，
∴在△ABD中，∠ABD=180°-90°-80°=10°；
（2）∵∠BDC是△ABD的外角，
∴∠EDC＞∠A，
又∵∠BEC是△CDE的外角，
∴∠BEC＞∠EDC，
∴∠BEC＞∠A．
∴∠A=80°，∠ABC=60°，
又∵BD⊥AC，
∴∠ADB=90°，
∴在△ABD中，∠ABD=180°-90°-80°=10°；
（2）∵∠BDC是△ABD的外角，
∴∠EDC＞∠A，
又∵∠BEC是△CDE的外角，
∴∠BEC＞∠EDC，
∴∠BEC＞∠A．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
