题目内容
【题目】如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=50°。
(1)求∠DAE的度数;
(2)试写出∠DAE与∠C、∠B之间的数量关系(不必说明理由)

【答案】(1)10°;(2)![]() .
.
【解析】
(1)根据三角形内角和定理求出∠BAC,再根据角平分线的定义求出∠BAD,根据直角三角形两锐角互余求出∠DAE,然后求解即可;
(2)分两种情况,利用(1)中的数据关系直接得出答案即可.
解:(1)∵∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=100°,
∵AE是角平分线,
∴∠BAE=![]() ∠BAC=
∠BAC=![]() ×100°=50°,
×100°=50°,
∵AD是高,
∴∠BAD=90°-∠B=90°-50°=40°,
∴∠DAE=∠BAE-∠BAD=40°-30°=10°.
(2)当∠C>∠B时,如图1,
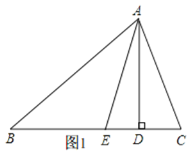
根据三角形的内角和得,∠BAC=180°-(∠B+∠C),
∵AD是角平分线,
∴∠BAD=![]() ∠BAC=90°-
∠BAC=90°-![]() [180°-(∠B+∠C)]=
[180°-(∠B+∠C)]= ![]() (∠B+∠C)-90°,
(∠B+∠C)-90°,
∵AE是△ABC的高,
∴∠BAE=90°-∠B,
∴∠DAE=∠BAE-∠BAD=90°-∠B-[![]() (∠B+∠C)-90°]=
(∠B+∠C)-90°]= ![]() (∠C-∠B),
(∠C-∠B),
∴∠DAE=![]() (∠C-∠B).
(∠C-∠B).
当∠C<∠B时,如图2,
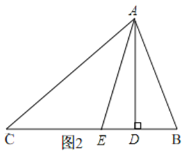
同∠B>∠C的方法得出,∠DAE=![]() (∠B-∠C).
(∠B-∠C).

练习册系列答案
相关题目