题目内容
【题目】如图，已知直线y=
x与双曲线y=
（k＞0）交于A，B两点，且点A的横坐标为4，
（1）求 k的值；
（2）利用图形直接写出不等式x＞的解；
（3）过原点O的另一条直线l交双曲线y=（k＞0）于P，Q两点（P点在第一象限），若由点 A，B，P，Q为顶点组成的四边形面积为 24，求点 P的坐标．
【答案】（1）8；（2）﹣4＜x＜0和x＞4．（3）点P的坐标为（8，1）或（2，4）．
【解析】（1）因为点A在直线y=
x上，故将其横坐标代入直线的解析式，求出对应的y的值，即可求得点A的坐标，再利用反比例函数图象上点的坐标特征即可求出k值；
（2）根据两函数图象的上下位置关系即可得出不等式的解集；
（3）作AM⊥x轴于点M，PN⊥x轴于点N．设P点的坐标为（a，8a），根据正比例函数与反比例函数的对称性即可得出四边形APBQ为平行四边形，结合四边形面积为24以及三角形的面积公式即可得出关于a的一元二次方程，解方程即可得出a值，将其代入点P的坐标中即可得出结论．
（1）∵直线y=
x与双曲线y=
（k＞0）交于A，B两点，且点A的横坐标为 4，
∴
×4=2，即：A点的坐标为（4，2），
∴k=4×2=8， 即：k的值为 8．
（2）∵点 A与点 B关于原点 O对称，
∴点B的坐标为（﹣4，﹣2），
又∵不等式x＞的解，是函数图象上直线位于双曲线上方的部分对应的x的取值，
∴由图象可知：不等式 x＞的解是：﹣4＜x＜0和x＞4．
（3）作AM⊥x轴于点M，PN⊥x轴于点N．设P点的坐标为（a，
）．
∵P、Q 关于 O 点对称，A、B 关于 O 点对称，
∴四边形 APBQ 为平行四边形，
∴4S△OAP=24
∴S△OAP=6．
①当点 P 在直线 AB 的下方时，如图 1 所示，
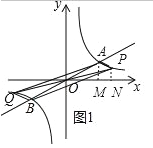
S△OAP=×4×2+
（
+2）（a﹣4）﹣a=6，
∴a2﹣6a﹣16=0，
解得：a1=﹣2，a2=8，
∴此时点P的坐标为（8，1）；
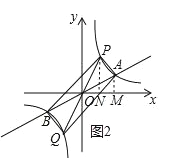
②当点 P 在直线 AB 的上方时，如图 2 所示，
S△OAP=a+
（+2）（4﹣a）﹣
×4×2=6，
∴a2+6a﹣16=0，
解得：a1=2，a2=﹣8，
∴此时点P的坐标为（2，4）．
综上所述：点P的坐标为（8，1）或（2，4）．
