题目内容
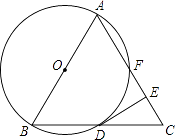
【题目】如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交BC的延长线于点F,若∠F=30°,DE=1,试求EF的长.

【答案】EF= 2.
【解析】
首先连接BE,由AB的垂直平分线DE交BC的延长线于F,可得AE=BE,又由在Rt△ABC中,∠ACB=90°,易求得∠A=∠F=∠ABE=∠CBE=30°,则可证得BE=EF,然后在Rt△BCE中,利用含30°角的直角三角形的性质,求得答案.
连接BE.
∵AB的垂直平分线DE交BC的延长线于F,∴AE=BE,∠A+∠AED=90°.
在Rt△ABC中,∵∠ACB=90°,∴∠FCE=90°,∴∠F+∠CEF=90°.
∵∠AED=∠FEC,∴∠A=∠F=30°,∴∠ABE=∠A=30°,∠ABC=90°﹣∠A=60°,∴∠CBE=∠ABC﹣∠ABE=30°,∴∠CBE=∠F,∴BE=EF.在Rt△BED中,BE=2DE=2×1=2,∴EF=2.

练习册系列答案
相关题目