题目内容
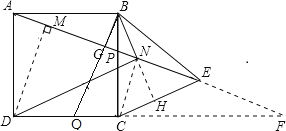
【题目】如图,在正方形ABCD中,点P、Q分别为BC、CD边上一点,且BP=CQ=![]() BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=
BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=![]() ,则CE的长为_____.
,则CE的长为_____.

【答案】![]()
【解析】分析:首先得出∠AGB=90°,过点D作DM⊥AN于M,根据五点共圆的性质得出Rt△DMN,Rt△BGN都是等腰直角三角形,然后根据DN的长度得出正方形的边长,根据△ABP的等积法得出BG的长度,然后根据△BGP和△CNP相似得出CN的长度,最后根据等腰直角三角形的性质得出CE的长度.
详解:∵BP=CQ,则△ABP≌△BCQ,∴∠AGB=90°,
连接CN,延长BN交CE于H. 过点D作DM⊥AN于M,
∴Rt△ADM≌Rt△ABG,DM=AG, ∵BN平分∠CBE,∴CH=HE,
∵∠CBN=∠EBN,BE=BC,BN=BN, ∴△BCN≌△BEN,
∴CN=NE,△CEN是等腰三角形,
延长AE交DC延长线于F,则有:∠BAG=∠BEG=∠CFE=∠BCN,
A,B,C,D,N五点共圆,∠AND=∠BNG=45°[AB弦所对圆周角=45°]
Rt△DMN,Rt△BGN都是等腰直角三角形,
∵DN=![]() , ∴AB=MN=
, ∴AB=MN=![]() ,根据△ABP的等积法可得:BG=
,根据△ABP的等积法可得:BG=![]() ,
,
∵△BGP∽△CNP,则CN=2BG=![]() ,则CE=
,则CE=![]() .
.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目