题目内容
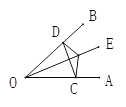
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
【答案】(1)证明见解析(2)证明见解析(3)证明见解析
【解析】试题分析:(1)根据角平分线性质可证ED=EC,从而可知△CDE为等腰三角形,可证∠ECD=∠EDC;
(2)由OE平分∠AOB,EC⊥OA,ED⊥OB,OE=OE,可证△OED≌△OEC,可得OC=OD;
(3)根据ED=EC,OC=OD,可证OE是线段CD的垂直平分线.
试题解析:证明:(1)∵OE平分∠AOB,EC⊥OA,ED⊥OB,∴ED=EC,即△CDE为等腰三角形,∴∠ECD=∠EDC;
(2)∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,∴∠DOE=∠COE,∠ODE=∠OCE=90°,OE=OE,∴△OED≌△OEC(AAS),∴OC=OD;
(3)∵OC=OD,且DE=EC,∴OE是线段CD的垂直平分线.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目