题目内容
【题目】(1)如图,直径是50cm圆柱形油槽装入油后,油深CD为15cm,求油面宽度AB的长.

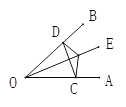
(2)如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F,连接CD.
①求证:四边形BCFE是菱形;
②在不添加任何辅助线和字母的情况下,请直接写出图中与△BEC面积相等的所有三角形(不包括△BEC).

【答案】(1)40(2)【1】证明见解析【2】△FEC、△AEB、△ADC、△BDC
【解析】(1)答案:40.
(2)【1】证明:∵D、E分别是AB、AC的中点,∴DE∥BC,BC=2DE.
∵CF∥BE,∴四边形BCFE是平行四边形.
∵BE=2DE,BC=2DE,∴BE=BC.∴BCFE是菱形;
【2】①∵由(1)知,四变形BCFE是菱形,∴BC=FE,BC∥EF,
∴△FEC与△BEC是等底等高的两个三角形,∴S△FEC=S△BEC.
②△AEB与△BEC是等底同高的两个三角形,则S△AEB=S△BEC.
③S△ADC=![]() S△ABC,S△BEC=
S△ABC,S△BEC=![]() S△ABC,则它S△ADC=S△BEC.
S△ABC,则它S△ADC=S△BEC.
④S△BDC=![]() S△ABC,S△BEC=
S△ABC,S△BEC=![]() S△ABC,则它S△BDC=S△BEC.
S△ABC,则它S△BDC=S△BEC.
综上所述,与△BEC面积相等的三角形有:△FEC、△AEB、△ADC、△BDC.


练习册系列答案
相关题目