Question

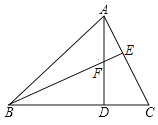
【题目】如图，在锐角中，，，的面积为33，点是射线上一动点，以为直径作圆交线段于点，交射线于点，交射线于点.

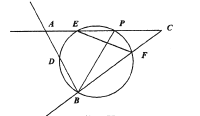
（1）当点在线段上时，若点为中点，求的长.

（2）连结，若为等腰三角形，求所有满足条件的值.

（3）将绕点顺时针旋转，当点的对应点恰好落在上时，记的面积为，的面积，则的值为__________（直接写出答案即可）.

Answer 1

【答案】(1);(2) 、2 、10;(3) .

【解析】

（1）连结，由为直径，得，由面积法解得BE=6，根据勾股定理得CE=8，所以，因为点为中点，所以，，，；

（2）需分类讨论， 分、、 ，①当时，连结因为，，所以， .

②当时，连结，因为，所以，，，③当时，连结，因为，，可证，所以.

(3) 过点C作CG⊥AB于点G, 过点E作EN⊥AB于点N, 过点E作EM⊥DP于点M, 过点E′作E′H⊥AB于点H,所以NEMD是矩形，根据面积易得CG，因为NE∥GC，E′H∥CG，所以得三角形相似，对应边成比例即可解答，具体过程见详解.

（1）连结，∵为直径，

∴，∴

，，

∵若点为中点，∴，

∵，∴，

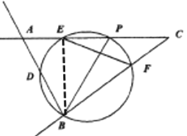
（2）情况1：，连结

∵，

，∴

情况2：，连结，，

∴，，

情况3：，连结，

∵，，∴，∴

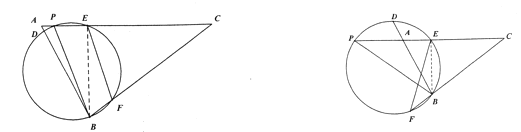
（3）过点C作CG⊥AB于点G, 过点E作EN⊥AB于点N, 过点E作EM⊥DP于点M, 过点E′作E′H⊥AB于点H,所以NEMD是矩形，S△ABC=×AB×CG,即 ×3×CG=33，解得CG= ,

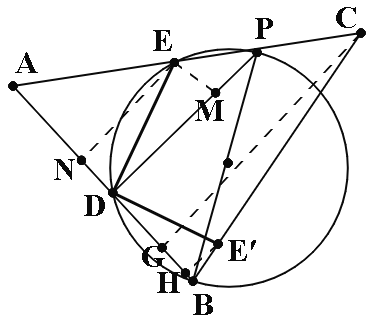
由（1）得：AE=3，∵NE∥GC，∴AE:AC=NE：GC，即3:11=NE：，解得：NE==DM，由勾股定理得AN=，

∵BP是直径，∴∠HDM=∠E′DE=90°，∠HDE′-∠E′DM =∠E′DE-∠E′DM，即∠HDE′=∠MDE，又∵DE′=DE，∠DHE′=∠DME=90°，∴△DHE′≌△DME,∴HE′=ME，DH= DM=， 所以 ==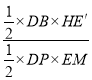 ，在Rt△BCG中，由勾股定理得：BG=,∵E′H∥CG，∴E′H：BH = CG：BG，即：E′H：BH=:=11：2，设E′H=11a，BH=2a,则E′H=11a=EM=ND，∵AN+ND+DH+HB=AB,即+11a++2a=3 ,解得：a=,∴DB=DH+HB=+2a=+2×=，AD=AN+ND=AN+HE′=+11a=

∵AN：AD=NE：DP, 即 ：= ：DP,∴DP=，∴==：

=.