题目内容
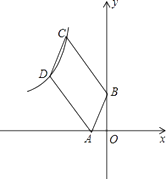
【题目】如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC= ![]() .
. 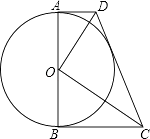
(1)求OD、OC的长;
(2)求证:△DOC∽△OBC;
(3)求证:CD是⊙O切线.
【答案】
(1)解:∵AD、BC是⊙O的两条切线,
∴∠OAD=∠OBC=90°,
在Rt△AOD与Rt△BOC中,OA=OB=3,AD=2,BC= ![]() ,
,
根据勾股定理得:OD= ![]() ,OC=
,OC= ![]()
(2)证明:过D作DE⊥BC,可得出∠DAB=∠ABE=∠BED=90°,
∴四边形ABED为矩形,
∴BE=AD=2,DE=AB=6,EC=BC﹣BE= ![]() ,
,
在Rt△EDC中,根据勾股定理得:DC= ![]() ,
,
∵ ![]() ,
,
∴△DOC∽△OBC;
(3)证明:过O作OF⊥DC,交DC于点F,
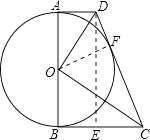
∵△DOC∽△OBC,
∴∠BCO=∠FCO,
∵在△BCO和△FCO中,
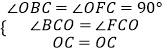 ,
,
∴△BCO≌△FCO(AAS),
∴OB=OF,
则CD是⊙O切线.
【解析】(1)由AB的长求出OA与OB的长,根据AD,BC为圆的切线,利用切线的性质得到三角形AOD与三角形BOC都为直角三角形,利用勾股定理即可求出OD与OC的长;(2)过D作DE垂直于BC,可得出BE=AD,DE=AB,在直角三角形DEC中,利用勾股定理求出CD的长,根据三边对应成比例的三角形相似即可得证;(3)过O作OF垂直于CD,根据(2)中两三角形相似,利用相似三角形的对应角相等得到一对角相等,利用AAS得到三角形OCF与三角形OCB全等,由全等三角形的对应边相等得到OF=OB,即OF为圆的半径,即可确定出CD为圆O的切线.
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案