题目内容
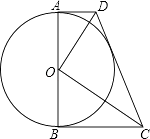
【题目】如图,在平面直角坐标系xOy中,直线y=k1x+b交x轴于点A(﹣3,0),交y轴于点B(0,2),并与y= ![]() 的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线.
的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线.
(1)求一次函数与反比例函数的解析式;
(2)若点C′是点C关于y轴的对称点,请求出△ABC′的面积.
【答案】
(1)
解:∵直线y=k1x+b交x轴于点A(﹣3,0),交y轴于点B(0,2),
∴ ![]() ,
,
解得 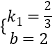 .
.
∴一次函数的解析式为y= ![]() x+2.
x+2.
∵OB是△ACD的中位线,OA=3,OB=2,∴OD=3,DC=4.
∴C(3,4).
∵点C在双曲线y= ![]() 上,
上,
∴k2=3×4=12.
∴反比例函数的解析式为y= ![]() .
.
(2)
解:∵点C′是点C(3,4)关于y轴的对称点,
∴C′(﹣3,4).
∴AC′⊥AO.
∴S△ABC′=S梯形AOBC′﹣S△ABO= ![]() (2+4)×3﹣
(2+4)×3﹣ ![]() 3×2=6.
3×2=6.
【解析】(1)根据直线y=k1x+b交x轴于点A(﹣3,0),交y轴于点B(0,2),代入解析式,求出k1和b的值,从而得出一次函数的解析式;再根据OB是△ACD的中位线,得出点C的坐标,最后代入双曲线y= ![]() ,即可求出反比例函数的解析式.(2)根据点C′是点C(3,4)关于y轴的对称点,求出C′的坐标,从而得出AC′⊥AO,最后根据S△ABC′=S梯形AOBC′﹣S△ABO , 代入计算即可.
,即可求出反比例函数的解析式.(2)根据点C′是点C(3,4)关于y轴的对称点,求出C′的坐标,从而得出AC′⊥AO,最后根据S△ABC′=S梯形AOBC′﹣S△ABO , 代入计算即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目