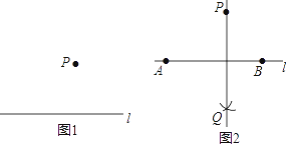题目内容
【题目】已知直线![]() (k>0)与双曲线
(k>0)与双曲线![]() (x>0)交于点M、N,且点N的横坐标为k. .
(x>0)交于点M、N,且点N的横坐标为k. .
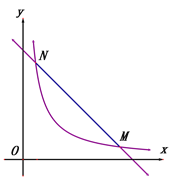
(1) 如图1,当k=1时.
①求m的值及线段MN的长;
②在y轴上是否是否存在点Q,使∠MQN=90°,若存在,请求出点Q的坐标;若不存在,请说明理由.
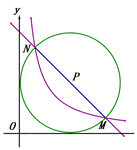
(2) 如图2,以MN为直径作⊙P,当⊙P与y轴相切时,求k值.
【答案】(1)①m=7;MN=6![]() ;②
;②![]() (3)k=
(3)k=![]() -3.
-3.
【解析】试题分析:(1)①根据题意直接代入即可求出m的值,然后求出M、N两点的坐标,根据勾股定理可求解;
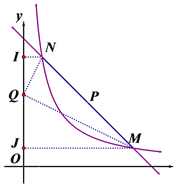
②如图,过M、N作y轴的垂线于J、I,设Q(0,t),由相似三角形的性质可求Q点的坐标;
(2)由双曲线与直线联立方程,得N(k,k+6), M(k+6,k),然后可求得MN的长,表示出P点的坐标,然后根据相切求出结果.
试题解析:(1) ① m=7,MN=6![]() 。
。
②存在,
如图,过M、N作y轴的垂线于J、I,设Q(0,t),
由相似三角形得![]() ,
,
解得![]() ,
,
所以Q点的坐标为![]() ,
, ![]() ;
;
(2)由双曲线与直线联立方程,得N(k,k+6), M(k+6,k),
求得MN=6![]() ,P(k+3,k+3),
,P(k+3,k+3),
∵⊙P与y轴相切,
∴k+3=![]() ,
,
所以k=![]() -3
-3

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目