题目内容
【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.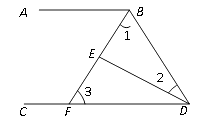
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFC的度数.
【答案】
(1)解:∵∠1+∠2=90°
∴∠DEB=∠DEF=90°
∵DE平分∠BDC
∴∠2=∠EDF,
又∵∠3+∠EDF=90°
∴∠3=∠1
∵BF平分∠ABD
∴∠1=∠ABF
∴∠ABF=∠3
∴AB∥CD
(2)解:∠BFC=115°
∵DE平分∠BDC,
∴∠EDF=∠2=25°,
∵∠1+∠2=90°,
∴∠FED=90°,
∴∠3=180°-90°-25°=65°.
∴∠BFC=180°-65°=115°.
【解析】(1)根据三角形的内角和由1+∠2=90°得出DEB=∠DEF=90°;进而得出∠3+∠EDF=90°,根据角平分线的定义得出2=∠EDF,1=∠ABF,从而得出∠ABF=∠3,根据内错角相等,两直线平行得出B//CD;
(2)根据角平分线的定义得出∠EDF=∠2=25°,根据三角形的外角和得出∠FED=∠1+∠2=90°,根据三角形的内角和得出∠3=180°-90°-25°=65°,根据邻补角的定义得出∠BFC=180°-65°=115°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目