题目内容
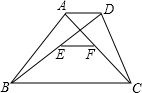
如图，在梯形ABCD中，AD∥BC，E、F分别是对角线BD、AC的中点，若AD=6cm，BC=18cm，则EF的长为（ ）
| A．8cm | B．7cm | C．6cm | D．5cm |
连接DF并延长，交BC于点K，
∵AD∥BC，
∴∠DAF=∠KCF，∠ADF=∠CKF，
∵E、F分别是对角线BD、AC的中点，
∴AF=CF，
在△ADF与△CKF中，
∵
，
∴△ADF≌△CKF（AAS），
∴DF=KF，CK=AD，
∴EF=
BK=
（BC-AD）=
×（18-6）=6（cm）．
故选C．
∵AD∥BC，
∴∠DAF=∠KCF，∠ADF=∠CKF，
∵E、F分别是对角线BD、AC的中点，
∴AF=CF，
在△ADF与△CKF中，
∵
|
∴△ADF≌△CKF（AAS），
∴DF=KF，CK=AD，
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选C．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
