题目内容
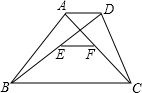
顺次连接一个任意四边形四边的中点，得到一个______四边形．
连接BD，
已知任意四边形ABCD，E、F、G、H分别是各边中点．
在△ABD中，E、H是AB、AD中点，
所以EH∥BD，EH=
BD．
在△BCD中，G、F是DC、BC中点，
所以GF∥BD，GF=
BD，
所以EH=GF，EH∥GF，
所以四边形EFGH为平行四边形．
故答案为：平行．
已知任意四边形ABCD，E、F、G、H分别是各边中点．
在△ABD中，E、H是AB、AD中点，
所以EH∥BD，EH=
| 1 |
| 2 |
在△BCD中，G、F是DC、BC中点，
所以GF∥BD，GF=
| 1 |
| 2 |
所以EH=GF，EH∥GF，
所以四边形EFGH为平行四边形．
故答案为：平行．
练习册系列答案
阅读快车系列答案
相关题目
