题目内容
【题目】为了满足学生的兴趣爱好，学校决定在七年级开设兴趣班，兴趣班设有四类：
围棋班；
象棋班；
书法班；
摄影班．为了便于分班，年级组随机抽查了部分学生的选课意向（每人选报一类），并绘制了如图所示的两幅统计图（不完整），请根据图中信息，解答下问题：
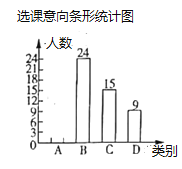
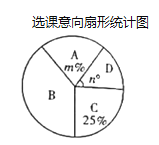
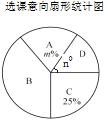
（1）求扇形统计图中
、
的值，并补全条形统计图；
（2）已知该校七年级有600名学生，学校计划开设三个“围棋班”，每班要求不超过40人，实行随机分班．
①学校的开班计划是否能满足选择“围棋班”的学生意愿，说明理由；
②展鹏、展飞是一对双胞胎，他们都选择了“围棋班”，并且希望能分到同一个班，用树状图或列表法求他们的希望得以实现的概率．
【答案】（1）m=20；
；补图见解析；（2）①能满足选择“围棋班”的学生意愿，理由见解析；②
．
【解析】
（1）利用C类人数除以其所占调查总人数的百分比即可求出调查总人数，然后利用调查总人数减去其余各类总人数即可求出A类人数，从而求出m的值，求出D类人数所占调查总人数的百分比乘360°即可求出n的值，最后补全条形统计图即可；
（2）①用600乘A类人数所占百分比最后除以3即可判断；
②根据题意，画出树状图，根据概率公式计算即可．
解：（1）
（人）
类人数为：
人
，
∴
，
∴
条形统计图补全如图．
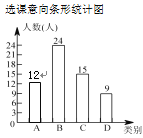
（2）①
，
∴能满足选择“围棋班”的学生意愿．
（3）树状图法：
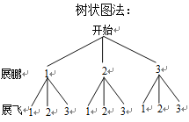
由图可知：共有9种等可能的结果，其中展鹏、展飞在同一个班的结果共有3种
∴
（展鹏、展飞同班）
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
