ЬтФПФкШн
ЁОЬтФПЁП2019ФъФГЦѓвЕАДВЭГјРЌЛјДІРэЗб25дЊ/ЖжЃЌНЈжўРЌЛјДІРэЗб16дЊ/ЖжБъзМЃЌЙВжЇИЖВЭГјКЭНЈжўРЌЛјДІРэЗб5200дЊЃЌДг2020ФъдЊдТЦ№ЃЌЪеЗбБъзМЩЯЕїЮЊВЭГјРЌЛјДІРэЗб100дЊ/ЖжЃЌНЈжўРЌЛјДІРэЗб30дЊ/ЖжЃЌШєИУЦѓвЕ2020ФъДІРэЕФетСНжжРЌЛјЪ§СПгы2019ФъЯрБШУЛгаБфЛЏЃЌОЭвЊЖржЇИЖРЌЛјДІРэЗб8800дЊ.
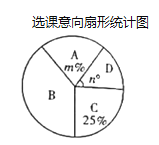
ЃЈ1ЃЉИУЦѓвЕ2019ФъДІРэЕФВЭГјРЌЛјКЭНЈжўРЌЛјИїЖрЩйЖжЃП
ЃЈ2ЃЉИУЦѓвЕМЦЛЎ2020ФъНЋЩЯЪіСНжжРЌЛјДІРэСПМѕЩйЕН240ЖжЃЌЧвНЈжўРЌЛјДІРэСПВЛГЌЙ§ВЭГјРЌЛјДІРэСПЕФ3БЖЃЌдђ2020ФъИУЦѓвЕзюЩйашвЊжЇИЖетСНжжРЌЛјДІРэЗбЙВЖрЩйдЊЃП
ЁОД№АИЁПЃЈ1ЃЉ2019ФъИУЦѓвЕДІРэЕФВЭГјРЌЛјЮЊ80ЖжЃЌНЈжўРЌЛјЮЊ200Жж.ЃЈ2ЃЉ11400дЊ.
ЁОНтЮіЁП
ЃЈ1ЃЉЩш2019ФъИУЦѓвЕДІРэЕФВЭГјРЌЛјЮЊxЖжЃЌНЈжўРЌЛјЮЊyЖжЃЌИљОнЬтвтСаГіЗНГЬзщЃЌНтДЫЗНГЬзщМДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉЩш2020ФъИУЦѓвЕДІРэЕФВЭГјРЌЛјЮЊaЖжЃЌНЈжўРЌЛјЮЊbЖжЃЌашжЇИЖЕФетСНжжРЌЛјДІРэЗбЪЧcдЊЃЌИљОнЁА2020ФъНЋЩЯЪіСНжжРЌЛјДІРэСПМѕЩйЕН240ЖжЃЌЧвНЈжўРЌЛјДІРэСПВЛГЌЙ§ВЭГјРЌЛјДІРэСПЕФ3БЖЁБПЩЧѓЕУaЕФШЁжЕЗЖЮЇЃЌдйСаГіcЙигкaЕФвЛДЮКЏЪ§ЃЌИљОнвЛДЮКЏЪ§ЕФдіМѕадМДПЩзїД№ЃЎ
НтЃКЃЈ1ЃЉЩш2019ФъИУЦѓвЕДІРэЕФВЭГјРЌЛјЮЊxЖжЃЌНЈжўРЌЛјЮЊyЖжЃЌИљОнЬтвтЕУ
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
МД2019ФъИУЦѓвЕДІРэЕФВЭГјРЌЛјЮЊ80ЖжЃЌНЈжўРЌЛјЮЊ200ЖжЃЎ
ЃЈ2ЃЉЩш2020ФъИУЦѓвЕДІРэЕФВЭГјРЌЛјЮЊaЖжЃЌНЈжўРЌЛјЮЊbЖжЃЌашжЇИЖЕФетСНжжРЌЛјДІРэЗбЪЧcдЊЃЌИљОнЬтвтЕУa+b=240ЧвbЁм3aЃЌ
НтЕУaЁн60ЃЎ
дђгаc=100a+30b=100a+30ЃЈ240-aЃЉ=70a+7200ЃЎ
гЩгкcЕФжЕЫцaЕФдіДѓЖјдіДѓЃЌ
ЫљвдЕБa=60ЪБЃЌcзюаЁЃЌзюаЁжЕЮЊ70ЁС60+7200=11400дЊЃЌ
МД2020ФъИУЦѓвЕзюЩйашвЊжЇИЖетСНжжРЌЛјДІРэЗбЙВ11400дЊЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ