ΧβΡΩΡΎ»ί
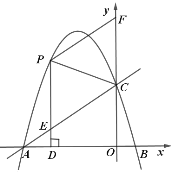
ΓΨΧβΡΩΓΩ≈ΉΈοœΏyΘΫax2+bx+cΘ®aΓΌ0Θ©”κx÷αΫΜ”ΎΒψAΘ®©¹1Θ§0Θ©Θ§BΘ®4Θ§0Θ©Θ§”κy÷αΫΜ”ΎΒψCΘ®0Θ§2Θ©Θ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
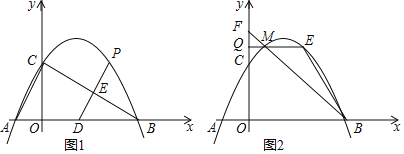
Θ®2Θ©»γΆΦ1Θ§ΒψDΒΡΉχ±ξΈΣΘ®2Θ§0Θ©Θ§ΒψP «ΗΟ≈ΉΈοœΏΒΎ“Μœσœό…œΒΡ“ΜΗωΕ·ΒψΘ§Ν§Ϋ”DPΫΜBC”ΎΒψEΘ°Β±ΓςBDE «Β»―ϋ»ΐΫ«–Έ ±Θ§÷±Ϋ”–¥≥ω¥Υ ±ΒψEΒΡΉχ±ξΘΜ
Θ®3Θ©»γΆΦ2Θ§ΒψMΘ®mΘ§nΘ© «≈ΉΈοœΏ…œΈΜ”ΎΕ‘≥Τ÷αΒΡΉσ≤ύ«“≤Μ‘ΎΉχ±ξ÷α…œΒΡΕ·ΒψΘ§ΙΐΒψMΉςx÷αΒΡΤΫ––œΏΫΜy÷α”ΎΒψQΘ§ΫΜ≈ΉΈοœΏ”ΎΝμ“ΜΒψEΘ§÷±œΏBMΫΜy÷α”ΎΒψFΘ§Β±SΓςMFQΘΚSΓςMEBΘΫ1ΘΚ3 ±Θ§«σ≥ωΒψMΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©ΒψEΒΡΉχ±ξΈΣ
ΘΜΘ®2Θ©ΒψEΒΡΉχ±ξΈΣ![]() Θ§
Θ§![]() Μρ
Μρ![]() Θ§
Θ§![]() Μρ
Μρ![]() ΘΜΘ®3Θ©ΒψMΒΡΉχ±ξΈΣ
ΘΜΘ®3Θ©ΒψMΒΡΉχ±ξΈΣ![]() Θ§
Θ§![]() Μρ
Μρ![]() Θ§
Θ§![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΒψ![]() Θ§
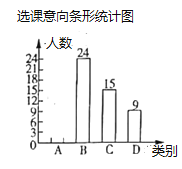
Θ§![]() Ήχ±ξ…η≥…≈ΉΈοœΏΫβΈω ΫΘ§‘ΌΫΪΒψ
Ήχ±ξ…η≥…≈ΉΈοœΏΫβΈω ΫΘ§‘ΌΫΪΒψ![]() Ήχ±ξ¥ζ»κ≈ΉΈοœΏΫβΈω Ϋ÷–Θ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Ήχ±ξ¥ζ»κ≈ΉΈοœΏΫβΈω Ϋ÷–Θ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
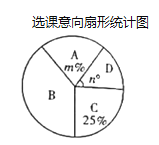
Θ®2Θ©œ»≈–Εœ≥ωΒψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§‘ΌΖ÷»ΐ÷÷«ιΩωΘ§άϊ”ΟΝΫΒψΦδΒΡΨύάκΙΪ ΫΘ§Ϋ®ΝΔΖΫ≥Χ«σΫβΦ¥Ω…ΒΟ≥ωΫα¬έΘΜ
…œΘ§‘ΌΖ÷»ΐ÷÷«ιΩωΘ§άϊ”ΟΝΫΒψΦδΒΡΨύάκΙΪ ΫΘ§Ϋ®ΝΔΖΫ≥Χ«σΫβΦ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®3Θ©œ»±μ Ψ≥ω![]() Θ§«σ≥ω÷±œΏ
Θ§«σ≥ω÷±œΏ![]() ΒΡΫβΈω ΫΘ§ΒΟ≥ωΒψ
ΒΡΫβΈω ΫΘ§ΒΟ≥ωΒψ![]() ΒΡΉχ±ξΘ§‘ΌΖ÷»ΐ÷÷«ιΩωΘ§άϊ”Ο
ΒΡΉχ±ξΘ§‘ΌΖ÷»ΐ÷÷«ιΩωΘ§άϊ”Ο![]() Θ§Ϋ®ΝΔΖΫ≥Χ«σΫβΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
Θ§Ϋ®ΝΔΖΫ≥Χ«σΫβΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
ΫβΘΚΘ®1Θ©![]() ≈ΉΈοœΏ
≈ΉΈοœΏ![]() ”κ
”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§
Θ§![]() Θ§
Θ§
![]() …η≈ΉΈοœΏΒΡΫβΈω ΫΈΣ
…η≈ΉΈοœΏΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
![]() ≈ΉΈοœΏ
≈ΉΈοœΏ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() ≈ΉΈοœΏΒΡΫβΈω ΫΈΣ
≈ΉΈοœΏΒΡΫβΈω ΫΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©![]() Βψ
Βψ![]() ‘Ύ≈ΉΈοœΏΒΎ“Μœσœό…œΒΡ“ΜΗωΕ·ΒψΘ§
‘Ύ≈ΉΈοœΏΒΎ“Μœσœό…œΒΡ“ΜΗωΕ·ΒψΘ§
![]() Βψ
Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§
…œΘ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() ÷±œΏ
÷±œΏ
![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
![]() «Β»―ϋ»ΐΫ«–ΈΘ§
«Β»―ϋ»ΐΫ«–ΈΘ§
![]() Β±
Β±![]() ±Θ§
±Θ§
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() Θ®…α
Θ®…α![]() Μρ
Μρ![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() Μρ
Μρ![]() Θ®…α
Θ®…α![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§
![]() Βψ
Βψ![]() «
«![]() ΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ§
ΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ§
![]() Βψ
Βψ![]() ΒΡΚαΉχ±ξ3Θ§
ΒΡΚαΉχ±ξ3Θ§
![]() Βψ
Βψ![]() Θ§
Θ§
Φ¥Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§
Θ§![]() Μρ
Μρ![]() Θ§
Θ§![]() Μρ
Μρ![]() ΘΜ
ΘΜ
Θ®3Θ©![]() Θ§
Θ§![]() Θ§
Θ§
![]() ≈ΉΈοœΏΒΡΕ‘≥Τ÷α÷±œΏΈΣ
≈ΉΈοœΏΒΡΕ‘≥Τ÷α÷±œΏΈΣ![]() Θ§
Θ§
![]() ÷αΘ§
÷αΘ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() ÷±œΏ
÷±œΏ![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() Θ®…α
Θ®…α![]() Μρ
Μρ![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() Θ®…α
Θ®…α![]() Μρ
Μρ![]() Θ®…α
Θ®…α![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() Μρ
Μρ![]() Θ®…α
Θ®…α![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
Φ¥Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§
Θ§![]() Μρ
Μρ![]() Θ§
Θ§![]() Θ§
Θ§

 «ßάο¬μΉΏœρΦΌΤΎΤΎΡ©Ζ¬’φ ‘ΨμΚ°ΦΌœΒΝ–¥πΑΗ
«ßάο¬μΉΏœρΦΌΤΎΤΎΡ©Ζ¬’φ ‘ΨμΚ°ΦΌœΒΝ–¥πΑΗ